
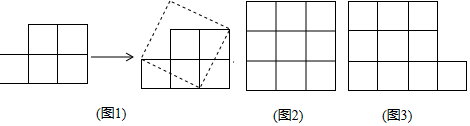
分析 (1)易得5个小正方形的边长的和,那么就得到了大正方形的面积,求得面积的算术平方根即可为大正方形的边长.
(2)利用勾股定理直接得出即可;
(3)一共有10个小正方形,那么组成的大正方形的面积为10,边长为10的算术平方根,在所给图形中截取两条长为$\sqrt{10}$的且互相垂直的线段,进而拼合即可.
解答 解:(1)∵小正方形的边长为1,
∴小正方形的面积为1,
∴大正方形的面积为5×1=5,
∴大正方形的边长为$\sqrt{5}$.
(2)如图2所示,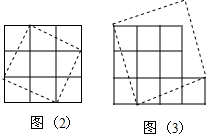 ;
;
(3)能,如图3所示,该正方形的边长=$\sqrt{10}$.
点评 此题主要考查了图形的剪拼以及勾股定理的应用,正确利用勾股定理得出是解题关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
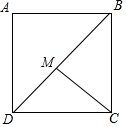 如图,在正方形ABCD中,M是对角线BD上一点,若AB=$\sqrt{2}$,则MD+2MC的最小值是$\sqrt{3}$+1,此时∠BMC=60度.
如图,在正方形ABCD中,M是对角线BD上一点,若AB=$\sqrt{2}$,则MD+2MC的最小值是$\sqrt{3}$+1,此时∠BMC=60度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com