
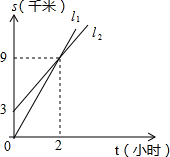
 A、B两人相距3千米,他们同时朝同一目的地匀速直行,并同时到达目的地,已知A的速度比B快,请根据图象进行判断:
A、B两人相距3千米,他们同时朝同一目的地匀速直行,并同时到达目的地,已知A的速度比B快,请根据图象进行判断:科目:初中数学 来源: 题型:解答题
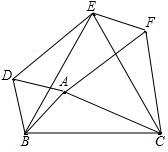 如图,已知以△ABC的三边为边,在BC的同侧分别作等边三角形ABD、BCE和ACF.
如图,已知以△ABC的三边为边,在BC的同侧分别作等边三角形ABD、BCE和ACF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
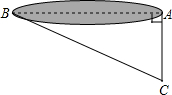 如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上点,测得BC=60m,AC=20m,则A,B两点问的距离40$\sqrt{2}$m.
如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上点,测得BC=60m,AC=20m,则A,B两点问的距离40$\sqrt{2}$m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
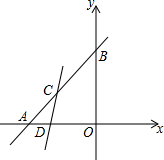 如图,S△AOB=18,且△AOB为等腰直角三角形,C为AB中点,过点C的直线l把△AOB面积分成5:1
如图,S△AOB=18,且△AOB为等腰直角三角形,C为AB中点,过点C的直线l把△AOB面积分成5:1查看答案和解析>>
科目:初中数学 来源: 题型:解答题
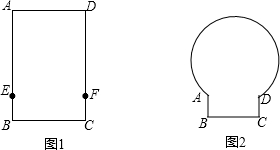
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
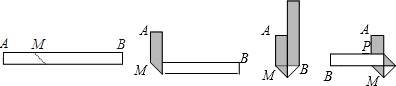
| A. | 7.5cm | B. | 9cm | C. | 10.5cm | D. | 12cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
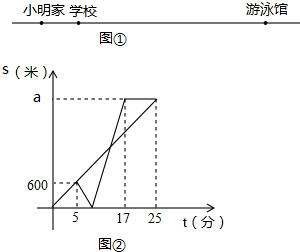 图①是小明家、学校和游泳馆之间的位置关系示意图,某天放学后,小亮和小明同时从学校出发,小亮匀速步行前往游泳馆,小明先匀速步行回家取游泳用品,然后骑自行车原路返回,沿与小亮相同的路线前往游泳馆,小明骑自行车的速度始终不变,小亮和小明各自与学校的距离s(米)与所用时间t(分)之间的函数图象的如图②所示.
图①是小明家、学校和游泳馆之间的位置关系示意图,某天放学后,小亮和小明同时从学校出发,小亮匀速步行前往游泳馆,小明先匀速步行回家取游泳用品,然后骑自行车原路返回,沿与小亮相同的路线前往游泳馆,小明骑自行车的速度始终不变,小亮和小明各自与学校的距离s(米)与所用时间t(分)之间的函数图象的如图②所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
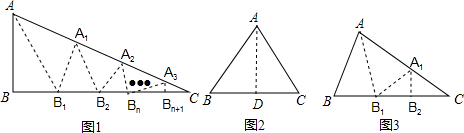
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com