
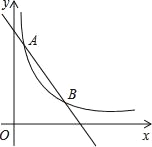
【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
【答案】(1)反比例函数的表达式y=![]() ,点B的坐标为(3,1).(2)
,点B的坐标为(3,1).(2)![]() .
.
【解析】试题分析:(1)由点A在一次函数图象上,结合一次函数解析式可求出点A的坐标,再由点A的坐标利用待定系数法即可求出反比例函数解析式,联立两函数解析式成方程组,解方程组即可求出点B坐标;
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,连接PB.由点B、D的对称性结合点B的坐标找出点D的坐标,设直线AD的解析式为y=mx+n,结合点A、D的坐标利用待定系数法求出直线AD的解析式,令直线AD的解析式中y=0求出点P的坐标,再通过分割图形结合三角形的面积公式即可得出结论.
试题解析:(1)把点A(1,a)代入一次函数y=-x+4,
得:a=-1+4,解得:a=3,
∴点A的坐标为(1,3).
把点A(1,3)代入反比例函数y=![]() ,
,
得:3=k,
∴反比例函数的表达式y=![]() ,
,
联立两个函数关系式成方程组得:  ,
,
解得: ![]() ,或
,或![]() ,
,
∴点B的坐标为(3,1).
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB的值最小,连接PB,如图所示.
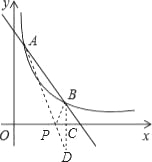
∵点B、D关于x轴对称,点B的坐标为(3,1),
∴点D的坐标为(3,- 1).
设直线AD的解析式为y=mx+n,
把A,D两点代入得: ![]() ,
,
解得: ![]() ,
,
∴直线AD的解析式为y=-2x+5.
令y=-2x+5中y=0,则-2x+5=0,
解得:x=![]() ,
,
∴点P的坐标为(![]() ,0).
,0).
S△PAB=S△ABD-S△PBD=![]() BD(xB-xA)-
BD(xB-xA)-![]() BD(xB-xP)
BD(xB-xP)
=![]() ×[1-(-1)]×(-1)-
×[1-(-1)]×(-1)-![]() ×[1-(-1)]×(3-
×[1-(-1)]×(3-![]() )
)
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:71=7,72=49,73=343,74=2 401,75=16 807,76=117 649,…,那么:71+72+73+…+72 016的末位数字是( )
A. 9B. 7C. 6D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数
3,9,27,81…①
1,3,9,27…②
2,10,26,82…③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)设x,y,z分别为第①②③ 行的2019个数,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是直角三角形,∠ACB=90°.
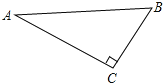
(1)尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母.
(2)在你按(1)中要求所作的图中,若BC=3,∠A=30°,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )

A. 14 B. 16 C. 17 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在坐标平面内,从点(x,y)移动到点(x+1,y+2)的运动称为一次A类跳马,从点(x,y)移动到点(x+2,y+1)的运动称为一次B类跳马.现在从原点开始出发,连续10次跳马,每次跳马采取A类或B类跳马,最后恰好落在直线![]() 上,则最后落马的坐标是_______.
上,则最后落马的坐标是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
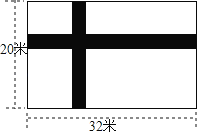
【题目】如图所示,宽为20米,长为32米的长方形地面上,修筑宽度为x米的两条互相垂直的小路,余下的部分作为耕地,如果要在耕地上铺上草皮,选用草皮的价格是每平米a元,
(1)求买草皮至少需要多少元?(用含a,x的式子表示)
(2)计算a=40,x=2时,草皮的费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com