
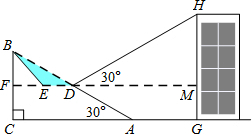
 如图,已知斜坡AB长60m,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.732).
如图,已知斜坡AB长60m,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.732).分析 (1)根据题意得出,∠BEF最大为45°,当∠BEF=45°时,EF最短,此时ED最长,进而得出EF的长,即可得出答案;
(2)利用在Rt△DPA中,DP=$\frac{1}{2}$AD,以及PA=AD•cos30°进而得出DM的长,利用HM=DM•tan30°得出即可.
解答 解:(1)∵修建的斜坡BE的坡角(即∠BEF)不大于45°,
∴∠BEF最大为45°,
当∠BEF=45°时,EF最短,此时ED最长,
∵∠DAC=∠BDF=30°,AD=BD=30,
∴BF=EF=$\frac{1}{2}$BD=15,
DF=15$\sqrt{3}$,
∴DE=DF-EF=15($\sqrt{3}$-1)=11.0(米);
故答案为:11.0.
(2)过点D作DP⊥AC,垂足为P,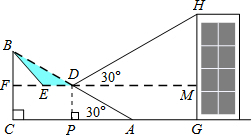
在Rt△DPA中,DP=$\frac{1}{2}$AD=$\frac{1}{2}$×30=15,
PA=AD•cos30°=$\frac{\sqrt{3}}{2}$×30=15$\sqrt{3}$.
在矩形DPGM中,MG=DP=15,DM=PG=15$\sqrt{3}$+27,
在Rt△DMH中,
HM=DM•tan30°=$\frac{\sqrt{3}}{3}$×(15$\sqrt{3}$+27)=15+9$\sqrt{3}$.
GH=HM+MG=15+15+9$\sqrt{3}$≈45.6.
答:建筑物GH高约为45.6米.
点评 此题主要考查了解直角三角形中坡角问题,根据图象构建直角三角形,进而利用锐角三角函数得出是解题关键.


科目:初中数学 来源: 题型:解答题
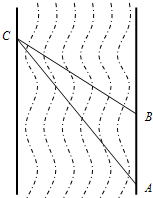 小明同学需测量一条河流的宽度(河岸两边互相平行).如图,小明同学在河岸一侧选取两个观测点A、B,在河对岸选取观测点C,测得AB=31m,∠CAB=37°,∠CBA=120°.请你根据以上数据,帮助小明计算出这条河的宽度.
小明同学需测量一条河流的宽度(河岸两边互相平行).如图,小明同学在河岸一侧选取两个观测点A、B,在河对岸选取观测点C,测得AB=31m,∠CAB=37°,∠CBA=120°.请你根据以上数据,帮助小明计算出这条河的宽度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
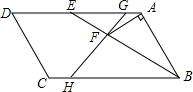 如图,?ABCD中,BE平分∠ABC,交AD于点E,AF⊥AB,交线段BE于点F,G为AE上一点,AG:GE=1:5,连结GF并延长交边BC于点H.若GE:BH=1:2,且AB=6,则BH=10;△AFG的面积=$\frac{{\sqrt{3}}}{2}$.
如图,?ABCD中,BE平分∠ABC,交AD于点E,AF⊥AB,交线段BE于点F,G为AE上一点,AG:GE=1:5,连结GF并延长交边BC于点H.若GE:BH=1:2,且AB=6,则BH=10;△AFG的面积=$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某学校教学楼从一楼到二楼由两段坡度相等的楼梯CA、AB联通(如图),经测量的这两层楼间的垂直高度BC为5米,∠BAC=70°,试求一楼到二楼的楼梯总长度(精确到0.1米).
某学校教学楼从一楼到二楼由两段坡度相等的楼梯CA、AB联通(如图),经测量的这两层楼间的垂直高度BC为5米,∠BAC=70°,试求一楼到二楼的楼梯总长度(精确到0.1米).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
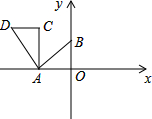 如图,直线y=$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,把△AOB绕点A逆时针旋转90°后得到△ACD,则点D的坐标是( )
如图,直线y=$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,把△AOB绕点A逆时针旋转90°后得到△ACD,则点D的坐标是( )| A. | (4,3) | B. | (-3,4) | C. | (-7,4) | D. | (-7,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com