
分析 (1)先将不等式左边因式分解,得出x(x-1)≥0,再根据乘法法则得出x与x-1同号,再分x与x-1同时为正号与同时为负号两种情况得出不等式组,解不等式组即可;
(2)先将不等式整理为x2-x-2<0,将左边因式分解,得出(x-2)(x+1)<0,再根据乘法法则得出x-2与x+1异号,再分x-2为正数与x-1为负数与x-2为负数与x-1为正数两种情况得出不等式组,解不等式组即可.
解答 解:(1)x2-x≥0,
x(x-1)≥0,
可化为$\left\{\begin{array}{l}{x≥0}\\{x-1≥0}\end{array}\right.$或$\left\{\begin{array}{l}{x≤0}\\{x-1≤0}\end{array}\right.$,
解得x≥1或x≤0.
故答案为x≥1或x≤0;
(2)x(x-1)<2,
x2-x-2<0,
(x-2)(x+1)<0,
可化为$\left\{\begin{array}{l}{x-2>0}\\{x+1<0}\end{array}\right.$或$\left\{\begin{array}{l}{x-2<0}\\{x+1>0}\end{array}\right.$,
解得无解或-1<x<2.
故答案为-1<x<2.
点评 本题考查了一元二次不等式的解法.含有一个未知数且未知数的最高次数为2的不等式叫做一元二次不等式.它的一般形式是 ax2+bx+c>0 或 ax2+bx+c<0(a不等于0).求一元二次不等式的解集实际上是将这个一元二次不等式的所有项移到不等式一侧并进行因式分解分类讨论求出解集.一元二次不等式还可通过二次函数图象进行求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ±4 | B. | 4或0 | C. | ±2 | D. | ±4或0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 上游1千米 | B. | 下游9千米 | C. | 上游10.3千米 | D. | 下游1千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
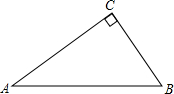 尺规作图题:如图△ABC中,∠C=90°
尺规作图题:如图△ABC中,∠C=90°查看答案和解析>>
科目:初中数学 来源: 题型:填空题
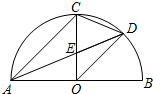 如图所示,AB是半圆形的直径,半径OC⊥AB于点O,AD平分∠CAB交$\widehat{BC}$于点D,连接CD,OD,给出以下四个结论:①AC∥OD;②CE=OE;③∠COD=∠DAB;④∠COD=∠CDA,其中正确结论的序号是①②④.
如图所示,AB是半圆形的直径,半径OC⊥AB于点O,AD平分∠CAB交$\widehat{BC}$于点D,连接CD,OD,给出以下四个结论:①AC∥OD;②CE=OE;③∠COD=∠DAB;④∠COD=∠CDA,其中正确结论的序号是①②④.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com