
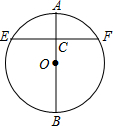
 如图,在⊙O中,直径AB的长度为4a,3AC=CB,过点C作EF⊥AB,交⊙O于点E,F,则EF的长度为2$\sqrt{3}$a.
如图,在⊙O中,直径AB的长度为4a,3AC=CB,过点C作EF⊥AB,交⊙O于点E,F,则EF的长度为2$\sqrt{3}$a.  同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
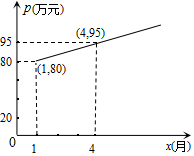 在气候对人类生存压力日趋加大的今天,发展低碳经济,全面实现低碳生活成为人们的共识,某企业采用技术革新,节能减排,经分析前5个月二氧化碳排放量y(吨)与月份x(月)之间的函数关系是y=-2x+50.
在气候对人类生存压力日趋加大的今天,发展低碳经济,全面实现低碳生活成为人们的共识,某企业采用技术革新,节能减排,经分析前5个月二氧化碳排放量y(吨)与月份x(月)之间的函数关系是y=-2x+50.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
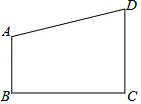 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的四边形,AB∥CD,CD⊥BC于C,且AB、BC、CD边长分别为2,4,3,则原直角三角形纸片的斜边长是4$\sqrt{5}$或10.
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的四边形,AB∥CD,CD⊥BC于C,且AB、BC、CD边长分别为2,4,3,则原直角三角形纸片的斜边长是4$\sqrt{5}$或10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
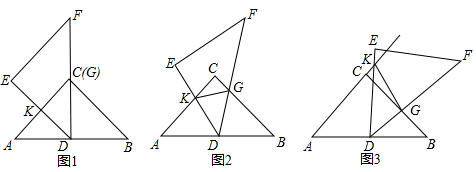
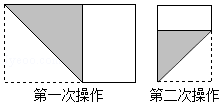 长为1,宽为a的矩形纸片($\frac{1}{2}$<a<1),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,求a的值.
长为1,宽为a的矩形纸片($\frac{1}{2}$<a<1),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,求a的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com