
 如图,已知AB=12;AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,求AE的长.
如图,已知AB=12;AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,求AE的长.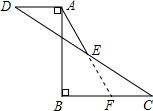 解:如图,延长AE交BC于F.
解:如图,延长AE交BC于F.
|
| AB2+BF2 |
| 122+52 |


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
 如图,已知AB=12,点C、D在AB上,且AC=DB=2,点P从点C沿线段CD向点D运动(运动到点D停止),以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF,连接EF,取EF的中点G,则下列说法中正确的有( )
如图,已知AB=12,点C、D在AB上,且AC=DB=2,点P从点C沿线段CD向点D运动(运动到点D停止),以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF,连接EF,取EF的中点G,则下列说法中正确的有( ) 查看答案和解析>>
科目:初中数学 来源:2012年河北香河实验初级中学第一次模拟初三数学试卷 题型:选择题
如图,已知AB=12,点C、D在AB上,且AC=DB=2,点P从点C沿线段CD向点D运
动(运动到点D停止),以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF,连
接EF,取EF的中点G,则下列说法中正确的有
①△EFP的外接圆的圆心为点G;②△EFP的外接圆与AB相切;
③四边形AEFB的面积不变;④EF的中点G移动的路径长为4
A.1个 B.2个 C.3个 D.4个

查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(新疆乌鲁木齐卷)数学 题型:填空题
如图,已知AB=12;AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,则AE的长是___________。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com