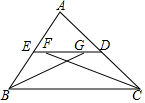
如图.在△ABC中.ED∥BC.∠ABC和∠ACB的平分线分别交ED于点G.F.若FG=2.ED=6.则EB+DC=8．题目和参考答案——青夏教育精英家教网—

3．

如图，在△ABC中，ED∥BC，∠ABC和∠ACB的平分线分别交ED于点G、F，若FG=2，ED=6，则EB+DC=8．

分析只要证明EG=EB，DF=DC即可解决问题．

解答解：∵ED∥BC，
∴∠EGB=∠GBC，∠DFC=∠FCB，
∵∠GBC=∠GBE，∠FCB=∠FCD，
∴∠EGB=∠EBG，∠DCF=∠DFC，
∴BE=EG，CD=DF，
∵FG=2，ED=6，
∴EB+CD=EG+DF=EF+FG+FG+DG=ED+FG=8，
故答案为8．

点评本题考查等腰三角形的判定和性质、角平分线的定义，平行线的性质等知识，解题的关键是等腰三角形的证明，属于基础题．

练习册系列答案

学习总动员单元复习专项复习期末复习系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

18．

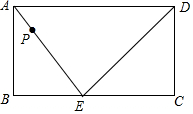如图，在矩形ABCD中，点E在BC边上，动点P以2厘米/秒的速度从点A出发，沿△AED的边按照A→E→D→A的顺序运动一周．设点P从A出发经x（x＞0）秒后，△ABP的面积是y．
（1）若AB=6厘米，BE=8厘米，当点P在线段AE上时，求y关于x的函数表达式；
（2）已知点E是BC的中点，当点P在线段AE上时，y=$\frac{12}{5}$x；当点P在线段AD上时，y=32-4x．求y关于x的函数表达式．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

19．立方是它本身的数是（　　）

A．

B．

C．

-1

D．

1，-1，0

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

11．

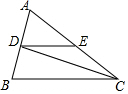如图，已知在△ABC中，CD平分∠ACB，且CD⊥AB于D，DE∥BC交AC于点E，AC=3cm，AB=2cm，则△ADE的周长为4cm．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

18．

如图，在平面直角坐标系中，点C在y轴上，点A（a，0）、点B（a-4，0），位于原点两侧，且∠ABC=60°，AE⊥BC，交y轴于点F，交BC于点E，点D在点B的左侧，且∠CDO=45°，AB=2BD
（1）直接写出∠BCD的度数、AB的长及点C的纵坐标（用含有a的式子表示）
①∠BCD=15°
②AB=4
③C（0，6-a）
（2）求∠ACD的度数；
（3）求点F的坐标（用含有a的式子表示）

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

8．

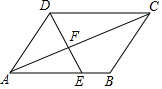如图，在平行四边形ABCD中，点E在边AB上，联结DE，交对角线AC于点F，如果$\frac{{S}_{△ADF}}{{S}_{△DFC}}$=$\frac{2}{3}$，CD=6，那么AE=4．