
【题目】在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
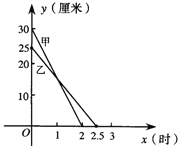
(1)甲、乙两根蜡烛燃烧前的高度分别是 ,从点燃到燃尽甲所用的时间为 .
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
(3)燃烧多长时间时,甲、乙两根蜡烛的高度相等(不考虑都燃尽时的情况)?在什么时间段内,甲蜡烛比乙蜡烛高?在什么时间段内,甲蜡烛比乙蜡低?
【答案】(1)30cm、25cm;2小时、2.5小时;(2)y甲=-15x+30,y乙=-10x+25.(3)燃烧1小时时,甲、乙两根蜡烛的高度相等;观察图象可以看出,当![]() 时,甲蜡烛比乙蜡烛高;当
时,甲蜡烛比乙蜡烛高;当![]() 时,甲蜡烛比乙蜡烛低.
时,甲蜡烛比乙蜡烛低.
【解析】
试题(1)由图象可知:甲、乙两根蜡烛燃烧前的高度分别是30cm、25cm,从点燃到燃尽所用的时间分别是2h、2.5h;(2)根据直线经过点的坐标列方程组解方程组即可求得函数解析式;(3)两直线的交点就是高度相同的时刻,根据图象即可解答.
试题解析:(1)甲、乙两根蜡烛燃烧前的高度分别是30厘米、25厘米,从点燃到燃尽所用的时间分别是2小时、2.5小时.
(2)设甲蜡烛燃烧时y与x之间的函数关系式为y=k1x+b1.
由图可知,函数的图象过点(2,0),(0,30),
∴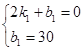 ,
,
解得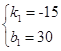
∴y=﹣15x+30
设乙蜡烛燃烧时y与x之间的函数关系式为y=k2x+b2.
由图可知,函数的图象过点(2.5,0),(0,25),
∴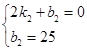 ,
,
解得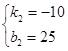
∴y=﹣10x+25;
由题意得﹣15x+30=﹣10x+25,解得x=1,
所以,当燃烧1小时的时候,甲、乙两根蜡烛的高度相等.
观察图象可知:当0≦x<1时,甲蜡烛比乙蜡烛高;
当1<x<2.5时,甲蜡烛比乙蜡烛低.


科目:初中数学 来源: 题型:
【题目】已知⊙O及⊙O外一点P,过点P作出⊙O的一条切线(只有圆规和三角板这两种工具),以下是甲、乙两同学的作业:
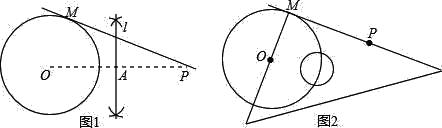
甲:①连接OP,作OP的垂直平分线l,交OP于点A;
②以点A为圆心、OA为半径画弧、交⊙O于点M;
③作直线PM,则直线PM即为所求(如图1).
乙:①让直角三角板的一条直角边始终经过点P;
②调整直角三角板的位置,让它的另一条直角边过圆心O,直角顶点落在⊙O上,记这时直角顶点的位置为点M;
③作直线PM,则直线PM即为所求(如图2).
对于两人的作业,下列说法正确的是( )
A. 甲乙都对B. 甲乙都不对
C. 甲对,乙不对D. 甲不对,已对
查看答案和解析>>
科目:初中数学 来源: 题型:
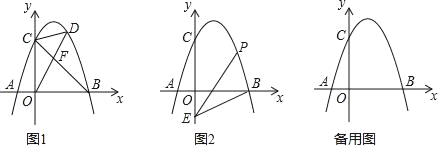
【题目】如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.
(1)求该抛物线的函数解析式.
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
(3)如图2,点E的坐标为(0,![]() ),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
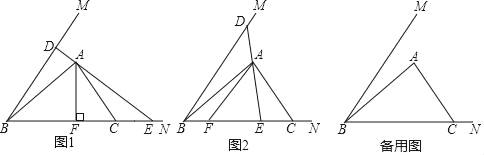
【题目】已知锐角∠MBN的余弦值为![]() ,点C在射线BN上,BC=25,点A在∠MBN的内部,且∠BAC=90°,∠BCA=∠MBN.过点A的直线DE分别交射线BM、射线BN于点D、E.点F在线段BE上(点F不与点B重合),且∠EAF=∠MBN.
,点C在射线BN上,BC=25,点A在∠MBN的内部,且∠BAC=90°,∠BCA=∠MBN.过点A的直线DE分别交射线BM、射线BN于点D、E.点F在线段BE上(点F不与点B重合),且∠EAF=∠MBN.
(1)如图1,当AF⊥BN时,求EF的长;
(2)如图2,当点E在线段BC上时,设BF=x,BD=y,求y关于x的函数解析式并写出函数定义域;
(3)联结DF,当△ADF与△ACE相似时,请直接写出BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批单价为4元的日用品,若按每件5元的价格销售,每天能卖出300件,若按每件6元的价格销售,每天能卖出200件,假定每天销售件数![]() (件)与价格
(件)与价格![]() (元/件)之间满足一次函数关系.
(元/件)之间满足一次函数关系.
(1)试求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)令每天的利润为![]() ,求出
,求出![]() 与
与![]() 之间的函数关系式;当销售价格定为多少时,才能使每天的利润最大?每天最大利润是多少?
之间的函数关系式;当销售价格定为多少时,才能使每天的利润最大?每天最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地被大山阻隔,若要从A地到B地,只能沿着如图所示的公路先从A地到C地,再由C地到B地.现计划开凿隧道A,B两地直线贯通,经测量得:∠CAB=30°,∠CBA=45°,AC=20km,求隧道开通后与隧道开通前相比,从A地到B地的路程将缩短多少?(结果精确到0.1km,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且BCP=ACD。
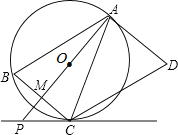
(1)判断直线PC与圆O的位置关系,并说明理由:
(2) 若AB=9,BC=6,求PC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
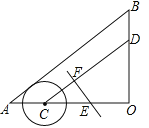
【题目】如图,△AOB中,∠O=90°,AO=8cm,BO=6cm,点C从A点出发,在边AO上以2cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以1.5cm/s的速度向O点运动,过OC的中点E作CD的垂线EF,则当点C运动了__s时,以C点为圆心,1.5cm为半径的圆与直线EF相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com