
已知:Rt△A′BC′≌Rt△ABC,∠A′C′B=∠ACB=90°,∠A′BC′=∠ABC=60°,Rt△A′BC′可绕点B旋转,设旋转过程中直线CC′和AA′相交于点D.
(1)如图1所示,当点C′在AB边上时,判断线段AD和线段A′D之间的数量关系,并证明你的结论;
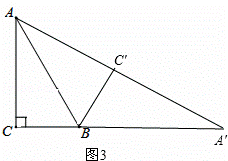
(2)将Rt△A′BC′由图1的位置旋转到图2的位置时,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
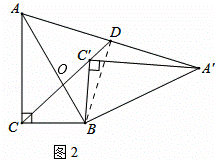
(3)将Rt△A′BC′由图1的位置按顺时针方向旋转α角(0°≤α≤120°),当A、C′、A′三点在一条直线上时,请直接写出旋转角的度数.
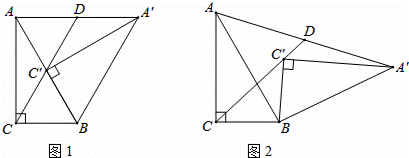
答:(1)AD=A′D.
证明:如图1,
∵Rt△A′BC′≌Rt△ABC,
∴BC=BC′,BA=BA′.
∵∠A′BC′=∠ABC=60°,
∴△BCC′和△BAA′都是等边三角形.
∴∠BAA′=∠BC′C=60°.
∵∠A′C′B=90°,
∴∠DC′A′=30°.
∵∠AC′D=∠BC′C=60°,
∴∠ADC′=60°.
∴∠DA′C′=30°.
∴∠DAC′=∠DC′A,∠DC′A′=∠DA′C′.
∴AD=DC′,DC′=DA′.
∴AD=A′D.
(2)AD=A′D
证明:连接BD,如图2,
由旋转可得:BC=BC′,BA=BA′,∠CBC′=∠ABA′.
∴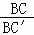 =
=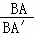 .
.
∴△BCC′∽△BAA′.
∴∠BCC′=∠BAA′.
∵∠BOC=∠DOA,
∴△BOC∽△DOA.
∴∠ADO=∠OBC,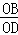 =
=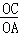 .
.
∵∠BOD=∠COA,
∴△BOD∽△COA.
∴∠BDO=∠CAO.
∵∠ACB=90°,
∴∠CAB+∠ABC=90°.
∴∠BDO+∠ADO=90°,即∠ADB=90°.
∵BA=BA′,∠ADB=90°,
∴AD=A′D.
(3)当A、C′、A′三点在一条直线上时,如图3,
则有∠AC′B=180°﹣∠A′C′B=90°.
在Rt△ACB和Rt△AC′B中,
 .
.
∴Rt△ACB≌Rt△AC′B (HL).
∴∠ABC=∠ABC′=60°.
∴当A、C′、A′三点在一条直线上时,旋转角α的度数为60°.


科目:初中数学 来源: 题型:
如图,直角 △ADB中,∠D=90°,C为AD上一点,且∠ACB 的度数为(5
的度数为(5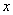 -10)°,则x的值可能是( )
-10)°,则x的值可能是( )
| A.10 | B.20 |
| C.30 | D.40 |
查看答案和解析>>
科目:初中数学 来源: 题型:
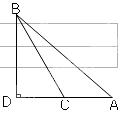
如图,已知点E、F在四边形ABCD的对角线延长线上,AE=CF,DE∥BF,∠1=∠2.
(1)求证: △AED≌△CFB;
△AED≌△CFB;
(2)若AD⊥CD,四边形ABCD是什么特殊四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
把标号分别为a,b,c的三个小球(除标号外,其余均相同)放在一个不透明的口袋中,充分混合后,随机地摸出一个小球,记下标号后放回,充分混合后,再随机地摸出一个小球,两次摸出的小球的标号相同的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
居民区内的“广场舞”引起媒体关注,辽宁都市频道为此进行过专访报道.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A.非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.

请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
在平行四边形ABCD中,点E在AD上,且AE:ED=3:1,CE的延长线与BA的延 长线交于点F,则S△AFE:S四边形ABCE为( )
长线交于点F,则S△AFE:S四边形ABCE为( )

|
| A. | 3:4 | B. | 4:3 | C. | 7:9 | D. | 9:7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com