
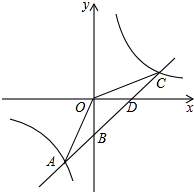
 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.分析 (1)利用待定系数法求出m,n,再求出直线AB的解析式以及点B坐标,根据S△AOC=S△AOB+S△OBC即可解决问题.
(2)根据一次函数图象在反比例函数图象下方,由此即可写出x的范围.
解答 解;(1)∵反比例函数y2=$\frac{m}{x}$的图象经过点A(-2,-5),
∴m=10,
∵C(5,n)在y=$\frac{10}{x}$上,
∴n=2,
∴$\left\{\begin{array}{l}{-2k+b=-5}\\{5k+b=2}\end{array}\right.$解得$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$,
∴点B坐标(0,-3),
∴S△AOC=S△AOB+S△OBC=$\frac{1}{2}$×3×2+$\frac{1}{2}$×3×5=$\frac{21}{2}$.
(2)根据图象,y1<y2时x的取值范围:x<-2或0<x<5.
点评 本题考查一次函数与反比例函数的图象的交点、待定系数法、三角形的面积等知识,解题的关键是利用一次函数的解析式求出点B坐标,学会分割法求面积,学会利用图象根据条件确定自变量的取值范围,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,3) | B. | (2,-3) | C. | (-2,-3) | D. | (-2,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 2013年 | 58 | 65 | 70 | 70 | 70 | 75 | 82 |
| 2014年 | 50 | 55 | 70 | 75 | 78 | 80 | 82 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 杂技团进行杂技表演,演员从跷跷板右端A处(OA=1米)弹跳到人梯顶端椅子B处,借助其弹性可以将演员弹跳到离地面最高处点P($\frac{5}{2}$,$\frac{19}{4}$)
杂技团进行杂技表演,演员从跷跷板右端A处(OA=1米)弹跳到人梯顶端椅子B处,借助其弹性可以将演员弹跳到离地面最高处点P($\frac{5}{2}$,$\frac{19}{4}$)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com