
(6分) 如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角
为45°,此时该同学距地面高度AE为20米,电梯再上升5米到达D点,此时测得大楼BC
楼顶B点的仰角为37º,求大楼的高度BC.(参考数据:sin37 º≈0.60, cos37 º≈0.80, tan37
º≈0.75)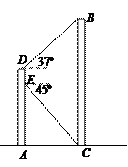
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
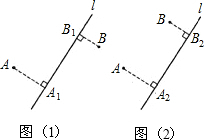 M与A1的距离是多少千米?
M与A1的距离是多少千米?查看答案和解析>>
科目:初中数学 来源: 题型:
 13、为了了解中学生的体能情况,抽取了某中学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布条形图,如图所示,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5.
13、为了了解中学生的体能情况,抽取了某中学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布条形图,如图所示,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5.查看答案和解析>>
科目:初中数学 来源: 题型:
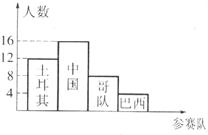 21、中国男子足球队44年来首次进入世界杯决赛圈,与巴西、土耳其、哥斯达黎加队同分在C组.6月3日,某班40名学生就C组哪支队伍将以小组第二名的身份进入十六强进行了竞猜,统计结果如图.若把认为中国队将以小组第二名的身份进入十六强的学生人数作为一组的频数,则这一组的频率为
21、中国男子足球队44年来首次进入世界杯决赛圈,与巴西、土耳其、哥斯达黎加队同分在C组.6月3日,某班40名学生就C组哪支队伍将以小组第二名的身份进入十六强进行了竞猜,统计结果如图.若把认为中国队将以小组第二名的身份进入十六强的学生人数作为一组的频数,则这一组的频率为查看答案和解析>>
科目:初中数学 来源: 题型:
| a2+24 |
| a2+24 |
查看答案和解析>>
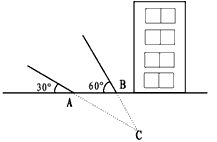
科目:初中数学 来源:吉林省期末题 题型:解答题
 、
、 、
、 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com