
【题目】如图,在平面直角坐标系中,已知点A的坐标是(4,0),且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.

(1)求抛物线的表达式;
(2)在抛物线上是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.
【答案】(1)抛物线的表达式是y=-x2+3x+4;(2)存在,点P的坐标为(-2,-6)或(2,6).
【解析】
试题分析:(1)先由已知条件求出B、C两点的坐标,再设抛物线的表达式是y=ax2+bx+c,将A,B,C三点的坐标代入,利用待定系数法即可求出抛物线的表达式;
(2)由(1)中所求解析式可设点P的坐标为(m,-m2+3m+4).当△ACP是以AC为直角边的直角三角形时,可分两种情况进行讨论:①以点A为直角顶点;②以点C为直角顶点;利用勾股定理分别列出关于m的方程,解方程即可.
试题解析:(1)∵点A的坐标是(4,0),
∴OA=4,
∵OA=OC=4OB,
∴OC=OA=4,OB=![]() OA=1,
OA=1,
∴点C的坐标是(0,4),点B的坐标是(-1,0).
设抛物线的表达式是y=ax2+bx+c,由题意得
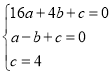 ,解得
,解得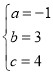 ,
,
∴抛物线的表达式是y=-x2+3x+4;
(2)存在.
设点P的坐标为(m,-m2+3m+4).
∵A(4,0),C(0,4),
∴AC2=42+42=32,AP2=(m-4)2+(-m2+3m+4)2,CP2=m2+(-m2+3m)2.
当△ACP是以AC为直角边的直角三角形时,可分两种情况:
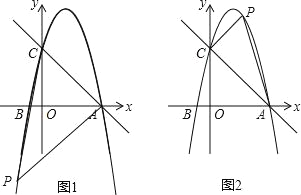
①如图1,如果点A为直角顶点,那么AC2+AP2=CP2,
即32+(m-4)2+(-m2+3m+4)2=m2+(-m2+3m)2,
整理得m2-2m-8=0,
解得m1=-2,m2=4(不合题意舍去),
则点P的坐标为(-2,-6);
②如图2,如果点C为直角顶点,那么AC2+CP2=AP2,
即32+m2+(-m2+3m)2=+(m-4)2+(-m2+3m+4)2,
整理得m2-2m=0,
解得m1=2,m2=0(不合题意舍去),
则点P的坐标为(2,6);
综上所述,所有符合条件的点P的坐标为(-2,-6)或(2,6).


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
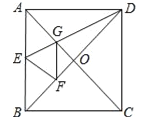
【题目】如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:①∠ADG=22.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG;⑥若S△OGF=1,则正方形ABCD的面积是![]() ,其中正确的结论个数为( )
,其中正确的结论个数为( )
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰△ABC,AC=BC=10.AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
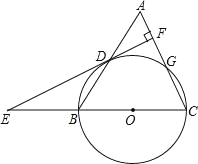
(1)求证:直线EF是⊙O的切线;
(2)求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6 cm,BC=8 cm,沿对角线AC将矩形分成两个直角三角形,其中△ABC不动,△A′C′D沿射线CA的方向以每秒2 cm的速度移动.
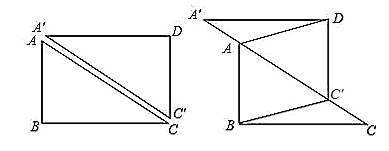
(1)在平移过程中,四边形ABC′D始终是 (请在下面的四个选项中选择一个你认为正确的序号填在横线上);
①平行四边形 ②矩形 ③菱形 ④正方形
(2)在移动过程中,当移动时间t(秒)为何值时,四边形ABC'D是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
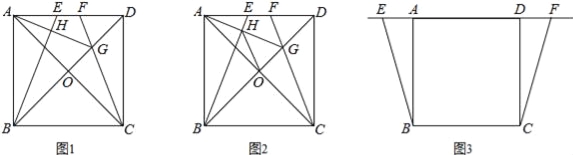
【题目】四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.
(1)如图1,当点E、F在线段AD上时,①求证:∠DAG=∠DCG;②猜想AG与BE的位置关系,并加以证明;
(2)如图2,在(1)条件下,连接HO,试说明HO平分∠BHG;
(3)当点E、F运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出∠BHO的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com