
【题目】如图,图1中小黑点的个数记为![]() ,图2中小黑点的个数记为
,图2中小黑点的个数记为![]() ,图3中小黑点的个数记为
,图3中小黑点的个数记为![]() ,…
,…
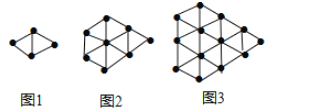
根据以上图中的规律完成下列问题:
(1)图4中小黑点的个数记为![]() ,则
,则![]() __________;
__________;
(2)图![]() 中小黑点的个数记为
中小黑点的个数记为![]() ,则
,则![]() ___________(用含
___________(用含![]() 的式子表示);
的式子表示);
(3)若第![]() 个图形中小黑点的个数比它前一个图形中小黑点的个数多100,则
个图形中小黑点的个数比它前一个图形中小黑点的个数多100,则![]() 的值是多少?
的值是多少?
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
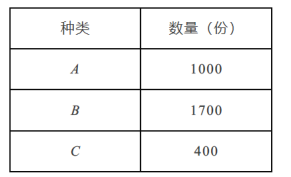
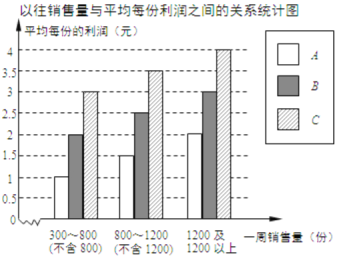
【题目】配餐公司为某学校提供A、B、C三类午餐供师生选择,三类午餐每份的价格分别是:A餐5元,B餐6元,C餐8元.为做好下阶段的营销工作,配餐公司根据该校上周A、B、C三类午餐购买情况,将所得的数据处理后,制成统计表(如下左图);根据以往销售量与平均每份利润之间的关系,制成统计图(如下右图).
请根据以上信息,解答下列问题:
(1)该校师生上周购买午餐费用的众数是 元;
(2)配餐公司上周在该校销售B餐每份的利润大约是 元;
(3)请你计算配餐公司上周在该校销售午餐约盈利多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在5月31日世界禁烟日到来之际,某校为了提高禁烟意识,在七、八年级举办了“关爱健康,远离香烟”的知识竞赛,两个年级分别有500人为了了解本次竞赛成绩情况,现从中各随机抽取了部分同学的测试成绩x(得分均为整数,满分为100分)进行调查分析,过程如下:
第一步:收集数据
七年级:68 88 100 100 79 94 89 85 100 88 81 69 98 79 77 94 96 75 92 67
八年级:69 97 78 89 98 100 99 100 95 99 99 69 75 100 99 78 79 87 85 79
第二步:整理、描述数据
分数段 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
七年级人数 | 3 | 4 | 5 | 8 |
八年级人数 | 2 | 5 | 3 | 10 |
第三步:分析数据
年级 | 平均数 | 中位数 | 众数 | 满分率 | 方差 |
七年级 | 86 | 88 | 100 | 15% | 115.6 |
八年级 | 88.7 | 92 | a | 15% | 120 |
第四步:应用数据
(1)直接写出a的值和八年级抽取了多少个同学的成绩进行分析
(2)在此次测试中,七年级甲学生的成绩为89分,八年级乙学生成绩为90分,甲、乙两人的成绩在各自年级中哪一个更靠前?请说明理由.
(3)若成绩在90分至99分之间(含90分,99分)的学生为二等奖,请估计七、八年级一共获得二等奖的学生总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
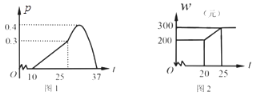
【题目】某农作物的生长率P与温度t(℃)有如下关系:如图1,当10≤t≤25时可近似用函数![]() 刻画;当25≤t≤37时可近似用函数
刻画;当25≤t≤37时可近似用函数![]() 刻画.
刻画.
(1)求h的值.
(2)按照经验,该作物提前上市的天数m(天)与生长率P满足函数关系:
生长率P | 0.2 | 0.25 | 0.3 | 0.35 |
提前上市的天数m(天) | 0 | 5 | 10 | 15 |
①请运用已学的知识,求m关于P的函数表达式;
②请用含![]() 的代数式表示m ;
的代数式表示m ;
(3)天气寒冷,大棚加温可改变农作物生长速度.在(2)的条件下,原计划大棚恒温20℃时,每天的成本为200元,该作物30天后上市时,根据市场调查:每提前一天上市售出(一次售完),销售额可增加600元.因此给大棚继续加温,加温后每天成本w(元)与大棚温度t(℃)之间的关系如图2.问提前上市多少天时增加的利润最大?并求这个最大利润(农作物上市售出后大棚暂停使用).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是__________.
的取值范围是__________.
(2)下表列出了![]() 与
与![]() 的几组对应值,请写出
的几组对应值,请写出![]() ,
,![]() 的值:
的值:![]() ________,
________,![]() ________.
________.
| … |
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | … |
| … |
|
|
|
|
|
|
| 2 |
|
|
| … |
(3)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象.
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象.
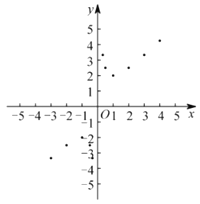
(4)结合函数的图象,请完成:
①当![]() 时,
时,![]() ________;
________;
②写出该函数的一条性质______________________________;
③若方程![]() 有两个相等的实数根,则
有两个相等的实数根,则![]() 的值是____________.
的值是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() .点
.点![]() 从
从![]() 点出发,沿
点出发,沿![]() 方向运动,以
方向运动,以![]() 为直径作
为直径作![]() ,当
,当![]() 运动到点
运动到点![]() 时停止运动,设
时停止运动,设![]() .
.
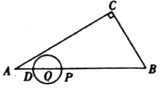
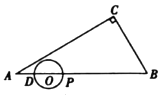
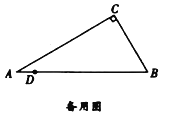
(1)![]() ___________,
___________,![]() ___________.(用
___________.(用![]() 的代数式表示)
的代数式表示)
(2)当![]() 为何值时,
为何值时,![]() 与
与![]() 的一边相切?
的一边相切?
(3)在点![]() 整个运动过程中,过点
整个运动过程中,过点![]() 作
作![]() 的切线交折线
的切线交折线![]() 于点
于点![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,过
,过![]() 作
作![]() 于
于![]() .
.
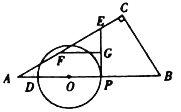

①当线段![]() 长度达到最大时,求
长度达到最大时,求![]() 的值;
的值;
②直接写出点![]() 所经过的路径长是________.(结果保留根号)
所经过的路径长是________.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+bx+c与x轴相交于A(-1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点C,作CD垂直x轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,且
边上一点,且![]() .点
.点![]() 是直线
是直线![]() 上一点且在点
上一点且在点![]() 的右侧,
的右侧,![]() ,点
,点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向以每秒1个单位长度的速度运动,设运动时间为
方向以每秒1个单位长度的速度运动,设运动时间为![]() 秒.以
秒.以![]() 为圆心,
为圆心,![]() 为半径作半圆
为半径作半圆![]() ,交直线
,交直线![]() 分别于点
分别于点![]() ,
,![]() (点
(点![]() 在
在![]() 的左侧).
的左侧).
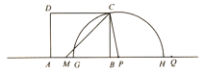
(1)当![]() 秒时,
秒时,![]()
![]() 的长等于__________,
的长等于__________,![]() __________秒时,半圆
__________秒时,半圆![]() 与
与![]() 相切;
相切;
(2)当点![]() 与点
与点![]() 重合时,求半圆
重合时,求半圆![]() 被矩形
被矩形![]() 的对角线
的对角线![]() 所截得的弦长;
所截得的弦长;
(3)若![]() ,求扇形
,求扇形![]() 的面积.
的面积.
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:将一个大于0的自然数,去掉其个位数字,再把剩下的数加上原数个位数字的4倍,如果得到的和能被13整除,则称这个数是“一刀两断”数,如果和太大无法直接观察出来,就再次重复这个过程继续计算,例如![]() ,所以55263是“一刀两断”数.
,所以55263是“一刀两断”数.![]() ,所以3247不是“一刀两断”数.
,所以3247不是“一刀两断”数.
(1)判断5928是否为“一刀两断”数:_____(填是或否),并证明任意一个能被13整除的数是“一刀两断”数;
(2)对于一个“一刀两断”数![]() 均为正整数),规定
均为正整数),规定![]()
![]() .若
.若![]() 的千位数字满是
的千位数字满是![]() ,千位数字与十位数字相同,且能被65整除,求出所有满足条件的四位数
,千位数字与十位数字相同,且能被65整除,求出所有满足条件的四位数![]() 中,
中,![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com