【题目】如图，长方形ABCD是由六个正方形组成的完美长方形，中间最小正方形的面积是1，最大正方形的边长为x.
(1)用x的代数式表示长方形ABCD的长是______或______、宽是______；
(2)求长方形ABCD的面积.
【答案】（1）2x1，3x8；2x3；（2）143.
【解析】
（1）设最大正方形的边长为x，依次表示出其余正方形的边长；
（2）根据组成长方形的上下对边相等列式求值得到最大正方形的边长，进而得到长方形的边长，求面积即可．
(1)∵中间最小正方形的面积是1，
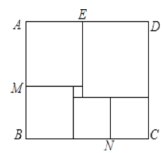
∴这个小正方形的边长为1，
∵最大正方形的边长为x，
∴AE=x1，
则：AD=x1+x=2x1，
∵AE=x1，
∴MB=x2，CN=x3，
∴BC=x2+x3+x3=3x8，AB=AM+MB=x1+x2=2x3；
故答案为：2x1，3x8；2x3；
(2)由题意得：2x1=3x8，
解得：x=7，
则AD=13，AB=11，
长方形ABCD的面积为：13×11=143，
答：长方形ABCD的面积为143.
科目：初中数学 来源： 题型：
【题目】如图，在边长为1个单位长度的小正方形网格中建立平面直角坐标系，已知
的顶点
的坐标为
，顶点
的坐标为
，顶点
的坐标为
.
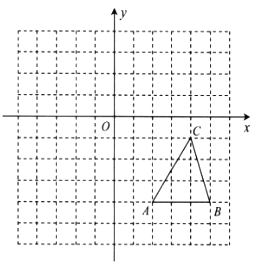
（1）求的面积；
（2）若把向上平移3个单位长度，再向左平移6个单位长度得到
，请画出；
（3）若点
在
轴上，且
的面积与的面积相等，请直接写出点的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成，硬纸板如图两种方法裁剪（裁剪后边角料不再利用）
A方法：剪6个侧面； B方法：剪4个侧面和5个底面。
现有38张硬纸板，裁剪时x张用A方法，其余用B方法。
（1）用x的代数式分别表示裁剪出的侧面和底面的个数；
（2）若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】从﹣3、﹣2、﹣1、1、2、3六个数中任选一个数记为k，若数k使得关于x的分式方程
＝k﹣2有解，且使关于x的一次函数y＝（k+
）x+2不经过第四象限，那么这6个数中，所有满足条件的k的值之和是（ ）
A. ﹣1B. 2C. 3D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校开设了丰富多彩的实践类拓展课程,分别设置了体育类、艺术类、文学类及其它类课程(要求人人参与,每人只能选择一门课程).为了解学生喜爱的拓展课类别,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题：
(1)此次共调查了多少人?
(2)请将条形统计图补充完整
(3)求文学类课程在扇形统计图中所占圆心角的度数；
(4)若该校有1500名学生,请估计喜欢体育类拓展课的学生人数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在菱形ABCD中，∠ABC＝60°，过点A作AE⊥CD于点E，交对角线BD于点F，过点F作FG⊥AD于点G．
（1）若AB＝2，求四边形ABFG的面积；
（2）求证：BF＝AE+FG．
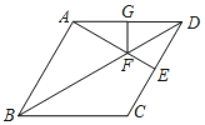
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，在
中，
平分
（
），
为上一点，且
于点
.
（1）当
，
时，求
的度数；
（2）若
，
，请结合（1）的计算猜想、
、
之间的数量关系，直接写出答案，不说明理由；（用含有
、
的式子表示）
（3）如图②，当点在的延长线上时，其余条件不变，则（2）中的结论还成立吗？若成立，请说明为什么；若不成立，请写出成立的结论，并说明为什么.
查看答案和解析>>
科目：初中数学 来源： 题型：
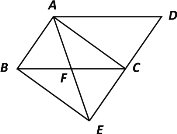
【题目】如图，将□ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F．
⑴求证：△ABF≌△ECF；⑵若∠AFC=2∠D，连接AC、BE．求证：四边形ABEC是矩形．
查看答案和解析>>
科目：初中数学 来源： 题型：
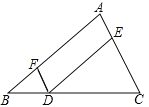
【题目】完成下面的证明，如图点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF∥CA．求证：∠FDE＝∠A．
证明：∵DE∥AB，
∴∠FDE＝∠ （ ）
∵DF∥CA，
∴∠A＝∠ （ ）
∴∠FDE＝∠A（ ）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com