(2003•宜昌)知识链接:
GPD是按市场价格计算的国内生产总值的简称.
百分点是百分比中相当于1%的单位,它是用“和”或“差”分析不同时期百分比的一种表示形式.如,工业总产值今年的增长幅度为19%(也可以说成增长了19个百分点),去年的增长幅度为16%,今年比去年的增长幅度增加了(19-16=3)3个百分点而不能说成增加了3%.
国债投资指国家发行长期建设国债的投资.它已成为经济稳定快速增长的助推器,据测算:每a元钱的国债投资带动的投资总额可以达到4a元至5a元.
问题思考:
2001年国债投资带动GDP增长1.7个百分点,创造了120万个就业单位;2002年国债投资1500亿元,创造了150万个就业岗位;从2000年到2002年的三年里,由于由国债投资带动GPD增长总共创造了400万个就业岗位.已知2000年与2002年由国债投资带动GPD增长百分点的和,比2001年由国债投资带动GPD增长百分点的两倍还多0.1
(1)若由国债投资带动的投资总额的40%将会转成劳务工资成为城乡居民的收入,请你估计2002年由国债投资带来的城乡居民收入的情况(数额范围);
(2)若每年GPD增长1.7个百分点就会创造120万个就业岗位,再每增加一个百分点就创造k万个就业岗位.请你确定比例系数k的值,并测算2002年由国债投资带动GPD增长了多少个百分点?
【答案】分析:(1)题中已知了02年的国债投资为1500亿元,根据“每a元钱的国债投资带动的投资总额可以达到4a元至5a元.”可计算出投资总额的范围.
然后根据“国债投资带动的投资总额的40%将会转成劳务工资成为城乡居民的收入”来计算出由国债投资带来的城乡居民收入.
(2)根据“2000年与2002年由国债投资带动GPD增长百分点的和,比2001年由国债投资带动GPD增长百分点的两倍还多0.1”,如果设2001年国债投资带动GDP新增长百分点为x,2002年国债投资带动GDP新增长百分点为y,那么可表示出y与x的函数关系式.
根据01年和02年创造的就业单位,我们可以用k分别根据01年和02年的投资情况表示出2000年的投资创造的就业单位的函数式.
然后根据这三个等式来求出自变量的值.
解答:解:(1)∵1500×40%×4=2400(亿元),1500×40%×5=3000(亿元),
∴2002年由国债投资带来的城乡居民收入为2400亿元至3000亿元.
(2)解:设2001年国债投资带动GDP新增长百分点为x,2002年国债投资带动GDP新增长百分点为y,根据题意,得
1.7+y=2x+0.1,①
130=120+k(x-1.7),②
150=120+k(y-1.7). ③
由①,得y=2x-1.6. ④
④代入③,得(2x-3.3)k=30. ⑤
由②:(x-1.7)k=10. ⑥
由⑤、⑥得x=1.8.
将x=1.8代入①,得y=2.
将x=1.8代入②,得k=100.
答:k=100,2002年由国债投资带动GDP新增长了2个百分点.
点评:本题中结合实际问题考查了一次函数的应用,本题中数量关系较多,读清题意是解题的关键.



 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案 倍时,你能确定k的值吗?若能,请求出k的值;若不能,请你说明理由.(图供分析参考用)
倍时,你能确定k的值吗?若能,请求出k的值;若不能,请你说明理由.(图供分析参考用)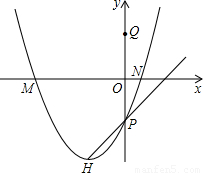
 倍时,你能确定k的值吗?若能,请求出k的值;若不能,请你说明理由.(图供分析参考用)
倍时,你能确定k的值吗?若能,请求出k的值;若不能,请你说明理由.(图供分析参考用)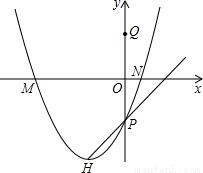
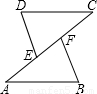
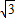 kx+k2-k+2=0,判别这个方程根的情况.”一题的解答过程,请你判断其是否正确,若有错误,请你写出正确解答.
kx+k2-k+2=0,判别这个方程根的情况.”一题的解答过程,请你判断其是否正确,若有错误,请你写出正确解答.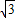 k)2-4×1×(k2-k+2)
k)2-4×1×(k2-k+2)