
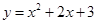 绕着原点旋转180°,所得抛物线的解析式是( ).
绕着原点旋转180°,所得抛物线的解析式是( ).| A.y=-(x-1)2-2 | B.y=-(x+1)2-2 |
C.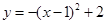 | D.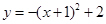 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:填空题
 轴交于
轴交于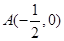 ,
,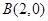 两点,且与
两点,且与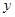 轴交于点
轴交于点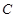 .
.
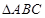 的形状为 ;
的形状为 ;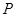 ,使得以
,使得以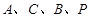 四点为顶点的四边形是梯形,则
四点为顶点的四边形是梯形,则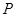 点的坐标为 .
点的坐标为 .查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
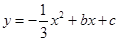 经过点A(6,0)、B(0,-4).
经过点A(6,0)、B(0,-4).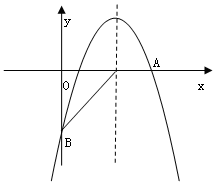
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
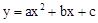 与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).
与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).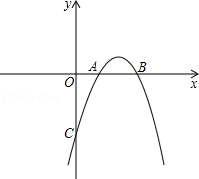
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
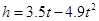 (的单位:秒,
(的单位:秒, 的单位:米)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
的单位:米)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )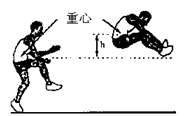
| A.0.71s | B.0.70s | C.0.63s | D.0.36s |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
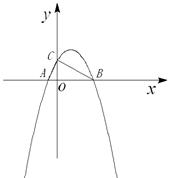
 经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=1200.
经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=1200.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com