Question

规定三角形的三条内角平分线的交点叫三角形的内心．
（1）已知I为三角形ABC的内心，连接AI交三角形ABC的外接圆于点D，如图所示，连接BD和CD，求证：BD=CD=ID．
（2）己知三角形ABC，AD平分∠BAC且与它的外接圆交于点D，在线段AD上有一点I满足BD=ID．试问点I是否是三角形ABC的内心？若是加以证明；若不是，说明理由．

Answer 1

（1）证明：

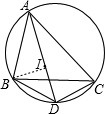
连接BI，
∵I是△ABC的内心，
∴∠BAD=∠DAC，∠ABI=∠CBI，
∴弧BD=弧DC，
∴BD=DC，
∵∠BID=∠ABI+∠BAD，∠IBD=∠CBI+∠DBC，
∵∠CAD=∠BAD=∠DBC，
∴∠DBI=∠BID，
∴BD=DI，
∴BD=CD=ID．

（2）答：I是三角形ABC的内心．
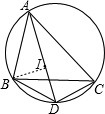
证明：连接BI，
∵∠BID=∠ABI+∠BAD，∠IBD=∠CBI+∠DBC，BD=ID，
∴∠BID=∠IBD，
∵AD平分∠BAC，
∴∠BAD=∠CAD=∠DBC，
∴∠ABI=∠CBI=∠BID-∠BAI，
∴∠ABI=∠CBI，
即I在∠ABC的平分线上，
即I是∠BAC何∠ABC的平分线的交点，
∴I也在∠ACB的角平分线上，
即I是三角形ABC的内心．
分析：（1）连接BI，根据三角形的内切圆的意义和圆周角定理得到BD=DC，根据三角形外角性质求出∠IBD=∠BID，根据等腰三角形的判定求出BD=ID即可；
（2）连接BI，根据等腰三角形的性质求出∠BID=∠IBD，推出∠ABI=∠CBI，得出I是∠BAC何∠ABC的平分线的交点即可．
点评：本题主要考查对等腰三角形的性质和判定，三角形的内切圆与内心，三角形的外角性质，圆周角定理，圆心角、弧、弦之间关系等知识点的理解和掌握，综合运用这些性质进行推理是解此题的关键．