
在平面直角坐标系中,抛物线 与x轴的两个交点分别为A(-3,0),B(1,0),过顶点C作CH⊥x轴于点H.
与x轴的两个交点分别为A(-3,0),B(1,0),过顶点C作CH⊥x轴于点H.



(1)a= ,b= ,顶点C的坐标为 .
(2)在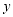 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由.
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由.
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标.
(1) ,
, ,C(﹣1,4);(2)存在,点D(0,3)或(0,1);(3)P(
,C(﹣1,4);(2)存在,点D(0,3)或(0,1);(3)P( ,
, )或(
)或( ,
, ).
).
【解析】
试题分析:(1)将A(﹣3,0)、B(1,0),代入 求出即可,再利用平方法求出顶点坐标即可;
求出即可,再利用平方法求出顶点坐标即可;
(2)首先证明△CED∽△DOA,得出y轴上存在点D(0,3)或(0,1),即可得出△ACD是以AC为斜边的直角三角形;
(3)首先求出直线CA的解析式为 ,再利用联立两函数解析式即可得出交点坐标,再利用若点P在对称轴左侧(如图②),只能是△PCQ∽△ACH,得∠PCQ=∠ACH得出答案即可.
,再利用联立两函数解析式即可得出交点坐标,再利用若点P在对称轴左侧(如图②),只能是△PCQ∽△ACH,得∠PCQ=∠ACH得出答案即可.
试题解析:(1)将A(﹣3,0)、B(1,0),代入 得:
得: ,解得:
,解得: ,
, ,∴
,∴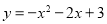 ,∴
,∴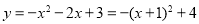 ,顶点C的坐标为(﹣1,4);
,顶点C的坐标为(﹣1,4);
(2)假设在y轴上存在满足条件的点D,过点C作CE⊥y轴于点E.由∠CDA=90°得,∠1+∠2=90°.又∠2+∠3=90°,∴∠3=∠1.又∵∠CED=∠DOA=90°,∴△CED∽△DOA,∴ .设D(0,c),则
.设D(0,c),则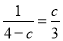 .变形得
.变形得 ,解之得
,解之得 ,
,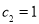 .综合上述:在y轴上存在点D(0,3)或(0,1),使△ACD是以AC为斜边的直角三角形;
.综合上述:在y轴上存在点D(0,3)或(0,1),使△ACD是以AC为斜边的直角三角形;
(3)①若点P在对称轴右侧(如图①),只能是△PCQ∽△CAH,得∠QCP=∠CAH.延长CP交x轴于M,∴AM=CM,∴ .设M(m,0),则
.设M(m,0),则 ,∴m=2,即M(2,0).设直线CM的解析式为
,∴m=2,即M(2,0).设直线CM的解析式为 ,则:
,则: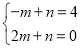 ,解得:
,解得: ,
, .∴直线CM的解析式为:
.∴直线CM的解析式为: .联立
.联立 ,解得:
,解得: 或
或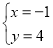 (舍去).∴P(
(舍去).∴P( ,
, ).
).
②若点P在对称轴左侧(如图②),只能是△PCQ∽△AHC,得∠PCQ=∠ACH.过A作CA的垂线交PC于点F,作FN⊥x轴于点N.由△CFA∽△CAH得 ,由△FNA∽△AHC得
,由△FNA∽△AHC得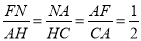 .∴AN=2,FN=1,CH=4,HO=1,则AH=2,∴点F坐标为(﹣5,1).设直线CF的解析式为
.∴AN=2,FN=1,CH=4,HO=1,则AH=2,∴点F坐标为(﹣5,1).设直线CF的解析式为 ,则
,则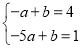 ,解得:
,解得: ,
, .∴直线CF的解析式为:
.∴直线CF的解析式为: .联立:
.联立: ,解得:
,解得: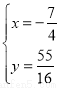 或
或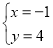 (舍去).∴P(
(舍去).∴P( ,
, ).
).
∴满足条件的点P坐标为( ,
, )或(
)或( ,
, ).
).

考点:1.二次函数综合题;2.压轴题.


科目:初中数学 来源:2014-2015学年广东省中山市九年级下学期开学检测数学试卷(解析版) 题型:选择题
已知两圆的半径R,r分别为方程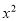 -5x+6=0的两根,两圆的圆心距为1,则两圆的位置关系是( )
-5x+6=0的两根,两圆的圆心距为1,则两圆的位置关系是( )
A.外离 B.内切 C.相交 D.外切
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省铜陵市四校九年级2月开学联考数学试卷(解析版) 题型:计算题
2014年1月23日,安徽省省政府新闻办召开新闻发布会,通报了2013年全省经济运行情况.据省统计局新闻发言人赵金宝介绍,去年我省GDP突破19000亿元,连续第十年保持两位数增长,增速明显高于全国,位居中部第一.初步核算,全年全省生产总值19033.3亿元,按可比价格计算,比2011年增加3303.3亿元,连续10年保持两位数增长,增幅居全国第11、中部第1位.求自2011年起的年平均增长率.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省铜陵市四校九年级2月开学联考数学试卷(解析版) 题型:填空题
如果圆锥的底面周长是20π,侧面展开后所得的扇形的圆心角为120°,那么圆锥的侧面积是__________.(结果保留π)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省安庆市九年级下学期正月联考数学试卷(解析版) 题型:解答题
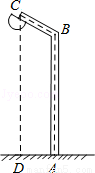
如图,用一根6米长的笔直钢管弯折成如图所示的路灯杆ABC,AB垂直于地面,线段AB与线段BC所成的角∠ABC=120°,若路灯杆顶端C到地面的距离CD=5.5米,求AB长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com