练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在一场足球比赛中，一球员从球门正前方10米处起脚射门，当球飞行的水平距离为6米时达到最高点，此时球高为3米．

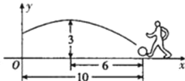
    （1）如图建立直角坐标系，当球飞行的路线为一抛物线时，求此抛物线的解析式．

    （2）已知球门高为2.44米，问此球能否射中球门（不计其它情况）．

    【答案】（1）y＝﹣（x﹣4）2+3；（2）能射中球门．

    【解析】

    （1）根据条件可以得到抛物线的顶点坐标是（4，3），利用待定系数法即可求得函数的解析式；

    （2）求出当x＝0时，抛物线的函数值，与2.44米进行比较即可判断．

    （1）抛物线的顶点坐标是（4，3），

    设抛物线的解析式是：y＝a（x﹣4）2+3，

    把（10，0）代入得36a+3＝0，

    解得a＝-，

    则抛物线是y＝﹣（x﹣4）2+3；

    （2）当x＝0时，y＝-×16+3＝3﹣＝＜2.44米．

    故能射中球门．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

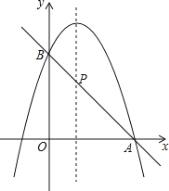
    【题目】如图，二次函数y=﹣x2+2x+m的图象过点A(3，0)，与y轴交于点B，直线AB与这个二次函数图象的对称轴交于点P．

    (1)求点B的坐标;

    (2)求点P的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一元二次方程2x2+2x﹣1=0的两个根为x1，x2，且x1＜x2，下列结论正确的是（　　）

    A. x1+x2=1 B. x1x2=﹣1 C. |x1|＜|x2| D. x12+x1=

    查看答案和解析>>

    科目：初中数学 来源： 题型：

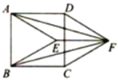
    【题目】如图，点E，F分别是正方形ABCD内部、外部的点，四边形ADFE与四边形BCFE均为菱形，连接AF，BF.有如下四个结论：①；②；③EF垂直平分DC；④；其中正确的是（ ）

    A.①②④B.①②③C.①③④D.①③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知菱形ABCD中，，点E是BC边上的一点（不与B，C重合），以BE为边构造菱形BEFG，使点G落在AB的延长线上，连接BD，GE，射线FE交BD于点H.

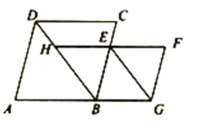
    （1）求证：四边形BGEH是平行四边形；

    （2）请从下面AB两题中任选一题作答，我选择______题.

    A.若四边形BGEH为菱形，则BD的长为_____.

    B.连接HC，CF，BF，若，且四边形BHCF为矩形，则CF的长为______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】淇淇和嘉嘉在学习了利用相似三角形测高之后分别测量两个旗杆高度.

    （1）如图1所示，淇淇将镜子放在地面上，然后后退直到她站直身子刚好能从镜子里看到旗杆的顶端E，测得脚掌中心位置B到镜面中心C的距离是50cm，镜面中心C距离旗杆底部D的距离为4m，已知淇淇同学的身高是1.54m，眼睛位置A距离淇淇头顶的距离是4cm，求旗杆DE 的高度.

    如图2所示，嘉嘉在某一时刻测得 1 米长的竹竿竖直放置时影长2米，在同时刻测量旗杆的影长时，旗杆的影子一部分落在地面上（BC），另一部分落在斜坡上（CD），他测得落在地面上的影长为10米，落在斜坡上的影长为米，∠DCE=45°，求旗杆AB的高度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知菱形的周长为20 cm，两对角线长度比为3：4，则对角线长分别为（ ）

    A.12cm．16cmB.6cm，8cmC.3cm，4cmD.24cm，32cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（2011山东济南，27，9分）如图，矩形OABC中，点O为原点，点A的坐标为（0，8），点C的坐标为（6，0）．抛物线经过A、C两点，与AB边交于点D．

    （1）求抛物线的函数表达式；

    （2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ=CP，连接PQ，设CP=m，△CPQ的面积为S．

    ①求S关于m的函数表达式，并求出m为何值时，S取得最大值；

    ②当S最大时，在抛物线的对称轴l上若存在点F，使△FDQ为直角三角形，请直接写出所有符合条件的F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】函数y＝的图象与直线y＝x+1没有交点，那么k的取值范围是_____．

    查看答案和解析>>

    同步练习册答案