【题目】如图，在ABCD中，AC，BD相交于点O，点E是OA的中点，连接BE并延长交AD于点F，已知S△AEF＝4，则下列结论：①
=
；②S△BCE＝36；③S△ABE＝12；④△AEF∽△ACD，其中正确结论是_________.（把正确结论的序号都填上）
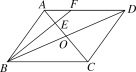
【答案】①②③
【解析】
根据平行四边形的性质得到
根据相似三角形的性质得到
等量代换得到
于是得到
；故①正确；根据相似三角形的性质得到S△BCE=36；故②正确；根据三角形的面积公式得到S△ABE=12，故③正确；由于△AEF与△ADC只有一个角相等，于是得到△AEF与△ACD不一定相似，故④错误．
解：∵在ABCD中，
∵点E是OA的中点，
∴
∵AD∥BC，
∴△AFE∽△CBE，
∴
∵AD=BC，
∴
∴ ；故①正确；
∵S△AEF=4， 
∴S△BCE=36；故②正确；
∵
∴
∴S△ABE=12，故③正确；
∵BF不平行于CD，
∴△AEF与△ADC只有一个角相等，
∴△AEF与△ACD不一定相似，故④错误，
故答案为：①②③．
科目：初中数学 来源： 题型：
【题目】如图所示，△ABC中，∠B=90°，AB=6cm，BC=8cm．
（1）点P从点A开始沿AB边向B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动．如果P，Q分别从A，B同时出发，经过几秒，使△PBQ的面积等于8cm2？
（2）点P从点A开始沿AB边向B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动．如果P，Q分别从A，B同时出发，线段PQ能否将△ABC分成面积相等的两部分？若能，求出运动时间；若不能说明理由．
（3）若P点沿射线AB方向从A点出发以1cm/s的速度移动，点Q沿射线CB方向从C点出发以2cm/s的速度移动，P，Q同时出发，问几秒后，△PBQ的面积为1？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，AB=2AD，点A（0，1），点C、D在反比例函数
（k＞0）的图象上，AB与x轴的正半轴相交于点E，若E为AB的中点，则k的值为_____．
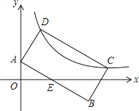
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】行驶中的汽车，在刹车后由于惯性的作用，还要向前方滑行一段距离才能停止，这段距离称为“刹车距离”，为了测定某种型号的汽车的刹车性能(车速不超过140 km/h)，对这种汽车进行测试，测得数据如下表：
刹车时车速/km·h－1 | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
刹车距离/m | 0 | 0.3 | 1.0 | 2.1 | 3.6 | 5.5 | 7.8 |
(1)以车速为x轴，以刹车距离为y轴，建立平面直角坐标系，根据上表对应值作出函数的大致图象；
(2)观察图象．估计函数的类型，并确定一个满足这些数据的函数解析式；
(3)该型号汽车在国道发生了一次交通事故，现场测得刹车距离为46.5 m，推测刹车时的车速是多少？请问事故发生时，汽车是超速行驶还是正常行驶？
查看答案和解析>>
科目：初中数学 来源： 题型：
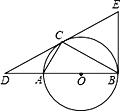
【题目】已知△ABC内接于以AB为直径的⊙O，过点C作⊙O的切线交BA的延长线于点D，且DA∶AB=1∶2．
（1）求∠CDB的度数；
（2）在切线DC上截取CE=CD，连接EB，判断直线EB与⊙O的位置关系，并证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
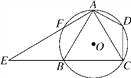
【题目】如图，已知四边形ABCD内接于⊙O，A是
的中点，AE⊥AC于A，与⊙O及CB的延长线交于点F，E，且
.
(1)求证：△ADC∽△EBA；
(2)如果AB＝8，CD＝5，求tan∠CAD的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
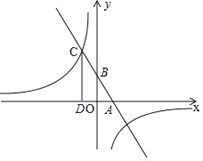
【题目】已知，如图，一次函数y＝kx+b（k、b为常数且k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y＝
，m为常数且m≠0）的图象在第二象限交于点C．若CD⊥x轴于D，若OA＝OD＝2，cos∠BAO＝
．
（1）求一次函数与反比例函数的解析式．
（2）若一次函数与反比例函数的另一个交点坐标为E，连接OC、OE，求△COE面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在某次数字变换游戏中，我们把整数0，1，2．…，100称为“旧数”，游戏的变换规则是：将旧数先平方，再除以100，所得到的数称为“新数”．
(1)请把旧数80和26按照上述规则变换为新数：
(2)经过上述规则变换后，我们发现许多旧数变小了．有人断言：“按照上述变换规则，所有的新数都不等于它的旧数．”你认为这种说法对吗?若不对，请求出所有不符合这一说法的旧数：
(3)请求出按照上述规则变换后减小了最多的旧数(要写出解答过程)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】
如图，在△ABC中，点E、D、F分别在边AB、BC、CA上，且DE∥CA，DF∥BA．下列四个判断中，不正确的是（ ）
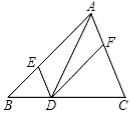
A．四边形AEDF是平行四边形
B．如果∠BAC=90°，那么四边形AEDF是矩形
C．如果AD平分∠BAC，那么四边形AEDF是矩形
D．如果AD⊥BC且AB=AC，那么四边形AEDF是菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com