
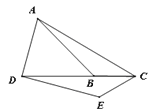
【题目】如图,在△ABC中,∠ACB=30°,将△ABC绕点C逆时针旋转得到△DEC,点A的对应点D恰好落在线段CB的延长线上,连接AD,若∠ADE=90°,则∠BAD=_________
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】把几个不同的数用大括号围起来,中间用逗号断开,如:{3,4},{-3,6,8,18},我们称之为集合,其中大括号内的数称其为集合的元素,如果一个集合满足:只要其中有一个元素a,使得-2a+4也是这个集合的元素,这样的集合我们称为条件集合,例如:集合{3,2},因为-2×3+4=-2,-2恰好是这个集合的元素,所以{3,-2}是条件集合:例如:集合{-2,9,8},因为-2×(-2)+4=8,8恰好是这个集合的元素,所以{-2,9,8}是条件集合.
(1)集合{-4,12}______条件集合;集合{![]() ,-
,-![]() ,
,![]() }______条件集合 (填“是”或“不是”)
}______条件集合 (填“是”或“不是”)
(2)若集合{8,10,n}是条件集合,求n的所有可能值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邻边不相等的矩形纸片,剪去一个正方形,余下一个四边形,称为第一次操作;在余下的四边形中减去一个正方形,又余下一个四边形,称为第二次操作;…,以此类推,若第n次操作后余下的四边形是正方形,则称原矩形是n阶矩形.如图,矩形ABCD中,若AB=1,AD=2,则矩形ABCD是1阶矩形.已知一个矩形是2阶矩形,较短边长为2,则较长边的长度为( )
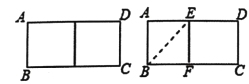
A. 6 B. 8 C. 5或8 D. 3或6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
如图,在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是( )
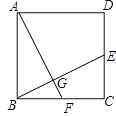
A.BE=AF B.∠DAF=∠BEC C.∠AFB+∠BEC=90° D.AG⊥BE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( )
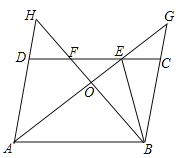
A. BO=OH B. DF=CE C. DH=CG D. AB=AE
查看答案和解析>>
科目:初中数学 来源: 题型:
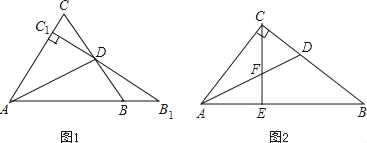
【题目】如图(1)所示:等边△ABC中,线段AD为其内角角平分线,过D点的直线B1C1⊥AC于C1交AB的延长线于B1.
(1)请你探究:![]() ,
,![]() 是否都成立?
是否都成立?
(2)请你继续探究:若△ABC为任意三角形,线段AD为其内角角平分线,请问![]() 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
(3)如图(2)所示Rt△ABC中,∠ACB=90,AC=8,AB=![]() ,DE∥AC交AB于点E,试求
,DE∥AC交AB于点E,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
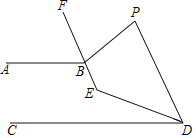
【题目】如图已知AB∥CD,P为直线AB,CD外一点,BF平分∠ABP,DE平分∠CDP,BF的反向延长线交DE于点E.
(1)∠ABP,∠P和∠PDC的数量关系为 ;
(2)若∠BPD=80°,求∠BED的度数;
(3)∠P与∠E的数量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
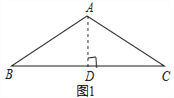
【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=![]() ∠BAC=60°,于是
∠BAC=60°,于是![]() ;
;
迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
(1)求证:△ADB≌△AEC;
(2)若AD=2,BD=3,请计算线段CD的长;
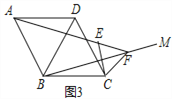
拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
(3)证明:△CEF是等边三角形;
(4)若AE=4,CE=1,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
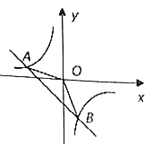
(1)试确定上述反比例函数和一次函数的表达式;
(2)当![]() 为何值时反比例函数值大于一次函数的值;
为何值时反比例函数值大于一次函数的值;
(3)当![]() 为何值时一次函数值大于比例函数的值;
为何值时一次函数值大于比例函数的值;
(4)求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com