
分析 根据x+y=6,xy=4,x>y,可以求得x-y的值,从而可以解答本题.
解答 解:∵x+y=6,xy=4,x>y,
∴x-y=$\sqrt{(x+y)^{2}-4xy}=\sqrt{{6}^{2}-4×4}=2\sqrt{5}$,
∴$\frac{\sqrt{x}-\sqrt{y}}{\sqrt{x}+\sqrt{y}}$
=$\frac{x-2\sqrt{xy}+y}{x-y}$
=$\frac{(x+y)-2\sqrt{xy}}{x-y}$
=$\frac{6-2\sqrt{4}}{2\sqrt{5}}$
=$\frac{\sqrt{5}}{5}$,
故答案为:$\frac{\sqrt{5}}{5}$.
点评 本题考查二次根式的化简求值,解题的关键是明确二次根式化简求值的方法.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:选择题
 如图,在同一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为5米,则这棵树的高度为( )
如图,在同一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为5米,则这棵树的高度为( )| A. | 7.8米 | B. | 3.2米 | C. | 2.3米 | D. | 1.5米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
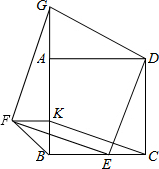 如图,四边形ABCD是正方形,点E、K分别在DC、AB上,CE=BK,点G在BA的延长线上,DG⊥DE.
如图,四边形ABCD是正方形,点E、K分别在DC、AB上,CE=BK,点G在BA的延长线上,DG⊥DE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com