
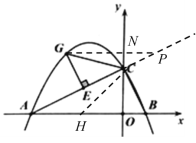
°æƒø°ø»ÁÕº£¨∂˛¥Œ∫Ø ˝![]() µƒÕºœÛΩª
µƒÕºœÛΩª![]() ÷·”⁄
÷·”⁄![]() °¢
°¢![]() ¡Ωµ„£¨Ωª
¡Ωµ„£¨Ωª![]() ÷·”⁄µ„
÷·”⁄µ„![]() £¨µ„
£¨µ„![]() Œ™∏√∂˛¥Œ∫Ø ˝ÕºœÛ∂•µ„£Æ¡¨Ω”
Œ™∏√∂˛¥Œ∫Ø ˝ÕºœÛ∂•µ„£Æ¡¨Ω”![]() °¢
°¢![]() º∞
º∞![]() °¢
°¢![]() £Æ
£Æ

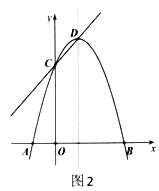

£®1£©»ÁÕº1£¨»Ùµ„![]() µƒ◊¯±Í
µƒ◊¯±Í![]() £¨∂•µ„
£¨∂•µ„![]() ◊¯±Í
◊¯±Í![]() £Æ
£Æ
¢Ÿ«Û![]() µƒ÷µ£¨≤¢Àµ√˜
µƒ÷µ£¨≤¢Àµ√˜![]() £ª
£ª
¢⁄»ÁÕº2£¨µ„![]() «≈◊ŒÔœþµƒ∂‘≥∆÷·…œ“ªµ„£¨“‘µ„
«≈◊ŒÔœþµƒ∂‘≥∆÷·…œ“ªµ„£¨“‘µ„![]() Œ™‘≤–ƒµƒ‘≤æ≠π˝
Œ™‘≤–ƒµƒ‘≤æ≠π˝![]() °¢
°¢![]() ¡Ωµ„£¨«“”Î÷±œþ
¡Ωµ„£¨«“”Î÷±œþ![]() œý«–£¨«Ûµ„
œý«–£¨«Ûµ„![]() µƒ◊¯±Í£ª
µƒ◊¯±Í£ª
£®2£©»Ù![]() £¨µ„
£¨µ„![]() £¨µ„
£¨µ„![]() £¨»ÁÕº3£¨∂ص„
£¨»ÁÕº3£¨∂ص„![]() ‘⁄÷±œþ
‘⁄÷±œþ![]() …œ∑Ωµƒ∂˛¥Œ∫Ø ˝ÕºœÛ…œ£Æπ˝µ„
…œ∑Ωµƒ∂˛¥Œ∫Ø ˝ÕºœÛ…œ£Æπ˝µ„![]() ◊˜
◊˜![]() ”⁄µ„
”⁄µ„![]() £¨ «∑ҥʑ⁄µ„
£¨ «∑ҥʑ⁄µ„![]() £¨ πµ√
£¨ πµ√![]() ÷–µƒƒ≥∏ˆΩ««°∫√µ»”⁄
÷–µƒƒ≥∏ˆΩ««°∫√µ»”⁄![]() µƒ2±∂£ø»Ù¥Ê‘⁄£¨«Û≥ˆµ„
µƒ2±∂£ø»Ù¥Ê‘⁄£¨«Û≥ˆµ„![]() µƒ∫·◊¯±Í£∫»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
µƒ∫·◊¯±Í£∫»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©¢Ÿ![]() £¨º˚Ω‚Œˆ£ª¢⁄µ„Pµƒ◊¯±ÍŒ™£®1£¨©Å4+
£¨º˚Ω‚Œˆ£ª¢⁄µ„Pµƒ◊¯±ÍŒ™£®1£¨©Å4+![]() £©ªÚ£®1£¨©Å4©Å
£©ªÚ£®1£¨©Å4©Å![]() £©£ª£®2£©Gµƒ∫·◊¯±Í
£©£ª£®2£©Gµƒ∫·◊¯±Í![]() ªÚ
ªÚ![]()
°æΩ‚Œˆ°ø
£®1£©¢Ÿ…Ë![]() £¨Ω´µ„B◊¯±Í¥˙»Î£¨«Û≥ˆa÷µ£¨µ√µΩ≈◊ŒÔœþ±Ì¥Ô Ω£¨¡Óy=0£¨«Û≥ˆµ„A◊¯±Í£¨∏˘æðOB∫ÕOCµ√≥ˆ°œCBO=°œOCB£¨‘Ÿ∏˘æð∏˜µ„◊¯±ÍÀ„≥ˆBC£¨DC£¨BDµƒ≥§£¨÷§√˜°˜BCD «÷±Ω«»˝Ω«–Œ£¨Õ∆≥ˆ°œDBC=°œOCA£¨¥”∂¯µ√µΩΩ·¬€£ª
£¨Ω´µ„B◊¯±Í¥˙»Î£¨«Û≥ˆa÷µ£¨µ√µΩ≈◊ŒÔœþ±Ì¥Ô Ω£¨¡Óy=0£¨«Û≥ˆµ„A◊¯±Í£¨∏˘æðOB∫ÕOCµ√≥ˆ°œCBO=°œOCB£¨‘Ÿ∏˘æð∏˜µ„◊¯±ÍÀ„≥ˆBC£¨DC£¨BDµƒ≥§£¨÷§√˜°˜BCD «÷±Ω«»˝Ω«–Œ£¨Õ∆≥ˆ°œDBC=°œOCA£¨¥”∂¯µ√µΩΩ·¬€£ª
¢⁄…Ë÷±œþCD«–°—P”⁄µ„E£Æ¡¨Ω·PE°¢PA£¨◊˜CF°ÕDQ”⁄µ„F£¨÷§√˜°˜DEPŒ™µ»—¸»˝Ω«–Œ£¨…ËP£®1£¨m£©£¨‘⁄°˜APQ÷–£¨¿˚”√π¥π…∂®¿Ì¡–≥ˆ∑Ω≥ã¨Ω‚≥ˆm£¨ø…µ√µ„P◊¯±Í£ª
£®2£©∑÷![]() £¨
£¨![]() ¡Ω÷÷«Èøˆ∑÷±Ã÷¬€£¨¡–≥ˆœý”¶∑Ω≥ã¨Ω‚÷ƺ¥ø….
¡Ω÷÷«Èøˆ∑÷±Ã÷¬€£¨¡–≥ˆœý”¶∑Ω≥ã¨Ω‚÷ƺ¥ø….
Ω‚£∫£®1£©¢Ÿ…Ë![]() £¨Ω´B£®3£¨0£©¥˙»Î£¨
£¨Ω´B£®3£¨0£©¥˙»Î£¨
Ω‚µ√![]() £¨
£¨
°ý≈◊ŒÔœþµƒΩ‚Œˆ Ω «£∫![]() £¨º¥
£¨º¥![]() £¨
£¨
¡Ó![]() £¨‘Ú
£¨‘Ú![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
°ýA£®£≠1£¨0£©£¨
°ý![]() £¨
£¨
°ý°œCBO=°œOCB£¨![]() £¨
£¨
°þ![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
°ý![]() £¨
£¨![]() «÷±Ω«»˝Ω«–Œ«“
«÷±Ω«»˝Ω«–Œ«“![]() £¨
£¨
°ý![]() £¨
£¨
”÷°þ°œDBC∫Õ°œOCA∂º «»ÒΩ«£¨
°ý°œDBC=°œOCA£¨
°ý°œDBA=°œACB£ª
¢⁄»ÁÕº£¨…Ë÷±œþCD«–°—P”⁄µ„E£Æ¡¨Ω·PE°¢PA£¨◊˜CF°ÕDQ”⁄µ„F£¨
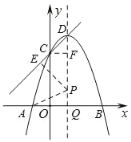
°ýPE°ÕCD£¨PE=PA£¨
”…y=©Åx2+2x+3£¨µ√£∫∂‘≥∆÷·Œ™÷±œþx=1£¨C£®0£¨3£©°¢D£®1£¨4£©£¨
°ýDF=4©Å3=1£¨CF=1£¨
°ýDF=CF£¨
°ý°˜DCFŒ™µ»—¸÷±Ω«»˝Ω«–Œ£¨
°ý°œCDF=45°„£¨
°ý°œEDP=°œEPD=45°„£¨
°ýDE=EP£¨
°ý°˜DEPŒ™µ»—¸»˝Ω«–Œ£¨
…ËP£®1£¨m£©£¨D£®1£¨4£©£¨
°ý![]() £¨
£¨
°ý![]() £¨
£¨
°ýEP2=![]() £®4©Åm£©2£¨
£®4©Åm£©2£¨
‘⁄°˜APQ÷–£¨°œPQA=90°„£¨
°ýAP2=AQ2+PQ2=[1-£®-1£©]2+m2
°ý![]() £®4©Åm£©2=[1-£®-1£©]2+m2£¨
£®4©Åm£©2=[1-£®-1£©]2+m2£¨
’˚¿Ì£¨µ√m2+8m©Å8=0£¨
Ω‚µ√£¨m=©Å4°¿![]() £¨
£¨
°ýµ„Pµƒ◊¯±ÍŒ™£®1£¨©Å4+![]() £©ªÚ£®1£¨©Å4©Å
£©ªÚ£®1£¨©Å4©Å![]() £©£ª
£©£ª
£®2£©Gµƒ∫·◊¯±Í![]() ªÚ
ªÚ![]() £¨
£¨
¢Ÿ»Ù![]() £¨
£¨
°ý![]() £¨
£¨
°ý![]() £¨
£¨
µ±![]() ±£¨
±£¨
![]() £¨
£¨
°ý![]() £¨
£¨
”⁄ «£¨![]() £¨
£¨
°ý![]() £¨
£¨
°ý![]() £¨
£¨
°ý![]() £®…·£©£¨
£®…·£©£¨![]() £¨
£¨
°ý![]() £ª
£ª
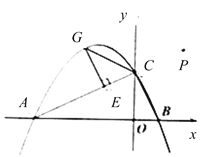
¢⁄»Ù![]() £¨
£¨
»°![]() µƒ÷–µ„
µƒ÷–µ„![]() £¨
£¨
‘Ú![]() £¨
£¨
°ý![]() £¨
£¨
°ý![]() £¨
£¨
¡Ó![]() £¨
£¨![]() £¨‘Ú
£¨‘Ú![]() £¨
£¨
°þ![]() £¨
£¨
°ý![]() £¨
£¨
°ý![]() £¨
£¨
°ý![]() £¨
£¨
°ý![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
°ý![]() £¨
£¨
°ý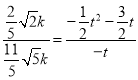 £¨
£¨
°ý![]() £¨
£¨
°ý![]()
𠵄Gµƒ∫·◊¯±Í![]() ªÚ
ªÚ![]() .
.


 染ª∑¥»˝Õ¨≤Ω«…Ω≤æ´¡∑œµ¡–¥∞∏
染ª∑¥»˝Õ¨≤Ω«…Ω≤æ´¡∑œµ¡–¥∞∏ ø⁄À„”Δ¶”√Âø®œµ¡–¥∞∏
ø⁄À„”Δ¶”√Âø®œµ¡–¥∞∏ √˚ ¶µ„æ¶◊÷¥ æ‰∂Œ∆™œµ¡–¥∞∏
√˚ ¶µ„æ¶◊÷¥ æ‰∂Œ∆™œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
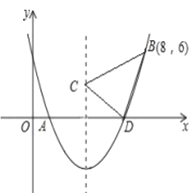
°æƒø°ø»ÁÕº£¨∂˛¥Œ∫Ø ˝![]() µƒÕºœÛΩª
µƒÕºœÛΩª![]() ÷·”⁄
÷·”⁄![]() ¡Ωµ„£¨≤¢æ≠π˝
¡Ωµ„£¨≤¢æ≠π˝![]() µ„£¨“—÷™
µ„£¨“—÷™![]() µ„◊¯±Í «
µ„◊¯±Í «![]() £¨
£¨![]() µ„◊¯±Í «
µ„◊¯±Í «![]() £Æ
£Æ
£®1£©«Û∂˛¥Œ∫Ø ˝µƒΩ‚Œˆ Ω£ª
£®2£©«Û∫Ø ˝ÕºœÛµƒ∂•µ„◊¯±Íº∞![]() µ„µƒ◊¯±Í£ª
µ„µƒ◊¯±Í£ª
£®3£©∂˛¥Œ∫Ø ˝µƒ∂‘≥∆÷·…œ «∑ҥʑ⁄“ªµ„![]() £¨ πµ√
£¨ πµ√![]() µƒ÷Ð≥§◊Ó–°£ø»Ù
µƒ÷Ð≥§◊Ó–°£ø»Ù![]() µ„¥Ê‘⁄£¨«Û≥ˆ
µ„¥Ê‘⁄£¨«Û≥ˆ![]() µ„µƒ◊¯±Í£¨»Ù
µ„µƒ◊¯±Í£¨»Ù![]() µ„≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
µ„≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øœ¬√Ê «–°√˜…˺∆µƒ°∞π˝÷±œþÕ‚“ªµ„◊˜’‚Ãı÷±œþµƒ∆Ω––œþ°±µƒ≥þπÊ◊˜Õºπ˝≥ãÆ
“—÷™£∫»ÁÕº1£¨÷±œþBCº∞÷±œþBCÕ‚“ªµ„P£Æ
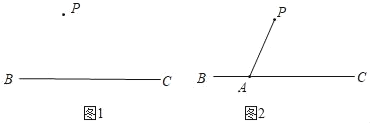
«Û◊˜£∫÷±œþPE£¨ πµ√PE°ŒBC£Æ
◊˜∑®£∫»ÁÕº2£Æ
¢Ÿ‘⁄÷±œþBC…œ»°“ªµ„A£¨¡¨Ω”PA£ª
¢⁄◊˜°œPACµƒ∆Ω∑÷œþAD£ª
¢€“‘µ„PŒ™‘≤–ƒ£¨PA≥§Œ™∞Îæ∂ª≠ª°£¨Ωª…‰œþAD”⁄µ„E£ª
¢Ð◊˜÷±œþPE£Æ
À˘“‘÷±œþPEæÕ «À˘«Û◊˜µƒ÷±œþ£Æ∏˘æð–°√˜…˺∆µƒ≥þπÊ◊˜Õºπ˝≥ãÆ
£®1£© π”√÷±≥þ∫Õ‘≤πÊ£¨≤π»´Õº–Œ£®±£¡Ù◊˜Õº∫€º££©£ª
£®2£©ÕÍ≥…œ¬√ʵƒ÷§√˜£Æ
÷§√˜£∫°þAD∆Ω∑÷°œPAC£¨
°ý°œPAD£Ω°œCAD£Æ
°þPA£ΩPE£¨
°ý°œPAD£Ω°° °°£¨
°ý°œPEA£Ω°° °°£¨
°ýPE°ŒBC£Æ£®°° °°£©£®ÃÓÕ∆¿Ì“¿æ𣩣Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨’˝∑Ω–ŒOABCµƒ“ª∏ˆ∂•µ„O «∆Ω√Ê÷±Ω«◊¯±Íœµµƒ‘≠µ„£¨∂•µ„A£¨C∑÷±‘⁄y÷·∫Õx÷·…œ£¨PŒ™±þOC…œµƒ“ª∏ˆ∂ص„£¨«“PQ°ÕBP£¨PQ=BP£¨µ±µ„P¥”µ„C‘À∂ØµΩµ„O ±£¨ø…÷™µ„Q º÷’‘⁄ƒ≥∫Ø ˝ÕºœÛ…œ‘À∂Ø£¨‘Ú∆‰∫Ø ˝ÕºœÛ «£® £©
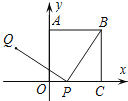
A.œþ∂ŒB.‘≤ª°
C.À´«˙œþµƒ“ª≤ø∑÷D.≈◊ŒÔœþµƒ“ª≤ø∑÷
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∏ßÀ≥ƒ≥÷–—ߌ™¡ÀΩ‚∞ÀƒÍº∂—ß…˙µƒÃƒÐ◊¥øˆ£¨¥”∞ÀƒÍº∂—ß…˙÷–Àʪ˙≥È»°≤ø∑÷—ß…˙Ω¯––ÃÐ≤‚ ‘£¨≤‚ ‘Ω·π˚∑÷Œ™A£¨B£¨C£¨DÀƒ∏ˆµ»º∂£Æ«Î∏˘æð¡Ω∑˘Õ≥º∆Õº÷–µƒ–≈œ¢ªÿ¥œ¬¡–Œ £∫
£®1£©±æ¥Œ≥È—˘µ˜≤Èπ≤≥È»°¡À∂ý…Ÿ√˚—ß…˙£ø
£®2£©«Û≤‚ ‘Ω·π˚Œ™Cµ»º∂µƒ—ß…˙ ˝£¨≤¢≤π»´Ãı–ŒÕº£ª
£®3£©»Ù∏√÷–—ß∞ÀƒÍº∂π≤”–700√˚—ß…˙£¨«Îƒ„π¿º∆∏√÷–—ß∞ÀƒÍº∂—ß…˙÷–ÃÐ≤‚ ‘Ω·π˚Œ™Dµ»º∂µƒ—ß…˙”–∂ý…Ÿ√˚£ø
£®4£©»Ù¥”ÃЌ™Aµ»º∂µƒ2√˚ƒ–…˙2√˚≈Æ…˙÷–Àʪ˙µƒ≥È»°2√˚—ß…˙£¨◊ˆŒ™∏√–£≈ý—¯‘À∂Ø‘±µƒ÷ÿµ„∂‘œÛ£¨«Î”√¡–±Ì∑®ªÚª≠ ˜◊¥Õºµƒ∑Ω∑®«ÛÀ˘≥È»°µƒ¡Ω»À«°∫√∂º «ƒ–…˙µƒ∏≈¬ £Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®∏–÷™£©»ÁÕº¢Ÿ£¨’˝∑Ω–Œ![]() ÷–£¨µ„
÷–£¨µ„![]() ‘⁄
‘⁄![]() ±þ…œ£¨
±þ…œ£¨![]() ∆Ω∑÷
∆Ω∑÷![]() £Æ»ÙŒ“√«∑÷±—”≥§
£Æ»ÙŒ“√«∑÷±—”≥§![]() ”Î
”Î![]() £¨Ωª”⁄µ„
£¨Ωª”⁄µ„![]() £¨‘Ú“◊÷§
£¨‘Ú“◊÷§![]() £Æ£®≤ª–Ë“™÷§√˜£©
£Æ£®≤ª–Ë“™÷§√˜£©
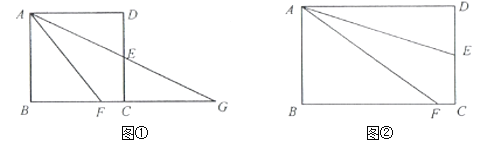
£®ÃΩæø£©»ÁÕº¢⁄£¨‘⁄æÿ–Œ![]() ÷–£¨µ„
÷–£¨µ„![]() ‘⁄
‘⁄![]() ±þµƒ÷–µ„£¨µ„
±þµƒ÷–µ„£¨µ„![]() ‘⁄
‘⁄![]() ±þ…œ£¨
±þ…œ£¨![]() ∆Ω∑÷
∆Ω∑÷![]() £Æ«Û÷§£∫
£Æ«Û÷§£∫![]() £Æ
£Æ
£®”¶”√£©‘⁄£®ÃΩæø£©µƒÃıº˛œ¬£¨»Ù![]() £¨
£¨![]() £¨÷±Ω”–¥≥ˆ
£¨÷±Ω”–¥≥ˆ![]() µƒ≥§£Æ
µƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–,∫Ø ˝![]() (x>0)µƒÕºœÛ”Î÷±œþl1:
(x>0)µƒÕºœÛ”Î÷±œþl1:![]() Ωª”⁄µ„A£¨”Î÷±œþl2£∫x=kΩª”⁄µ„B£Æ÷±œþl1”Îl2Ωª”⁄µ„C£Æ
Ωª”⁄µ„A£¨”Î÷±œþl2£∫x=kΩª”⁄µ„B£Æ÷±œþl1”Îl2Ωª”⁄µ„C£Æ

(1) µ±µ„Aµƒ∫·◊¯±ÍŒ™1 ±£¨‘Ú¥À ±kµƒ÷µŒ™ _______£ª
(2) ∫·°¢◊ð◊¯±Í∂º «’˚ ˝µƒµ„Ω–◊ˆ’˚µ„£Æ º«∫Ø ˝![]() (x>0) µƒÕºœÒ‘⁄µ„A°¢B÷ƺ‰µƒ≤ø∑÷”Îœþ∂ŒAC£¨BCŒß≥…µƒ«¯”Ú(≤ª∫¨±þΩÁ)Œ™W£Æ
(x>0) µƒÕºœÒ‘⁄µ„A°¢B÷ƺ‰µƒ≤ø∑÷”Îœþ∂ŒAC£¨BCŒß≥…µƒ«¯”Ú(≤ª∫¨±þΩÁ)Œ™W£Æ
¢Ÿµ±k=3 ±£¨Ω·∫œ∫Ø ˝ÕºœÒ£¨‘Ú«¯”ÚWƒ⁄µƒ’˚µ„∏ˆ ˝ «_________£ª
¢⁄»Ù«¯”ÚWƒ⁄«°”–1∏ˆ’˚µ„£¨Ω·∫œ∫Ø ˝ÕºœÛ£¨÷±Ω”–¥≥ˆkµƒ»°÷µ∑∂Œß£∫___________£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡ÀΩ‚ƒ≥ –≥ı÷–—ß…˙øŒÕ‚‘ƒ∂¡«Èøˆ£¨µ˜≤È–°◊È∂‘∏√ –’‚—ß∆⁄≥ı÷–—ß…˙‘ƒ∂¡øŒÕ‚ ȺƵƒ≤· ˝Ω¯––¡À≥È—˘µ˜≤È£¨≤¢∏˘æðµ˜≤ÈΩ·π˚ªÊ÷∆≥…»Áœ¬Õ≥º∆Õº£Æ
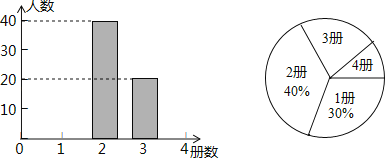
∏˘æðÕ≥º∆ÕºÃ·π©µƒ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
£®1£©±æ¥Œ≥È—˘µ˜≤ȵƒ—˘±æ»ð¡ø «°°°°£ª
£®2£©≤π»´Ãı–ŒÕ≥º∆Õº£ª
£®3£©∏√ –π≤”–12000√˚≥ı÷–…˙£¨π¿º∆∏√ –≥ı÷–—ß…˙’‚—ß∆⁄øŒÕ‚‘ƒ∂¡≥¨π˝2≤·µƒ»À ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
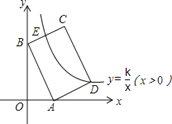
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨æÿ–ŒABCDµƒ±þAB£∫BC=3£∫2£¨µ„A£®3£¨0£©£¨B£®0£¨6£©∑÷±‘⁄x÷·£¨y÷·…œ£¨∑¥±»¿˝∫Ø ˝y=![]() £®x£æ0£©µƒÕºœÛæ≠π˝µ„D£¨«“”αþBCΩª”⁄µ„E£¨‘Úµ„Eµƒ◊¯±ÍŒ™__£Æ
£®x£æ0£©µƒÕºœÛæ≠π˝µ„D£¨«“”αþBCΩª”⁄µ„E£¨‘Úµ„Eµƒ◊¯±ÍŒ™__£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com