分析:根据⊙O
1的半径为5,⊙
2的半径为
,公共弦为AB,两圆的圆心的连线与公共弦的交点为C;那么根据相交两圆的定理,可出现来两个直角三角形为△O
1AC和△O
2AC,再利用勾股定理可分别求出O
1C和O
2C,然后分圆心在公共弦的同侧和异侧两种情况,根据求出O
1C和O
2C相加和相减即可求出相应的O
1O
2.
解答: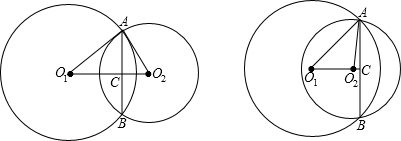
解:根据两圆相交的定理,可得O
1O
2⊥AB,且C为AB的中点,即AC=
AB=3,
在Rt△O
1AC中,O
1C=
=
=4,
同理,在Rt△O
2AC中,O
2C=
=
=2,
∴O
1O
2=O
1C+O
2C=4+2=6,
还有一种情况,O
1O
2=O
1C-O
2C=4-2=2.
故答案为:6或2
点评:本题综合运用了相交两圆的性质和勾股定理.注意此题的两种情况,因为圆心距都在两圆相交的这一范围内,都符合.根据题意画出相应的图形是解题的关键.