
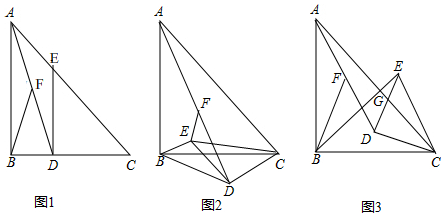
���� ��1���ڵ���ֱ�������Ρ�DEC�У����DC����Rt��ABD�У����ù��ɶ�������߶�AD��������б�����߶������ɽ�����⣮
��2����ͼ2�У��ӳ�EF��N��ʹ��FN=EF������BN���ӳ�DE��AB��M���ɡ�AFN�ա�DFE���Ƴ�AN=DE=DC����FAN=��FDE���Ƴ�DM��AN���Ƴ���OMB=��BAN���ɡ�MOB+��OMB=90�㣬��DOC+��COD=90�㣬��MOB=��DOC���Ƴ���OMB=��OCD���Ƴ���BAN=��BCD���Ƴ���BAN�ա�BCD���Ƴ���ABN=��CBD��BN=BD���Ƴ���DBN=��CBA=90�㣬��֤����BEN�ա�BED���Ƴ�DE=EN=2EF�����ɽ�����⣮
��3����ͼ3�У�����AE���ӳ�CD��AB��M����BC��ȡһ��N��ʹ��NM=NC����BM=m������֤����DBM�ס�ABD���Ƴ���BAD=��BDM=30�㣬�Ƴ���ABD=��ADB=75�㣬�Ƴ�AB=AD����ͼ4����BH��AD��H����BH��ȡһ��G��ʹ��BG=DG����DH=a����취��a��ʾBF2��BD2���ɽ�����⣮
��� ��1���⣺��ͼ1�У�
�ڵ���Rt��CDE�У��ߡ�CDE=90�㣬DE=DC��CE=2$\sqrt{2}$��
��DE=DC=2��
��AB=BC=3��
��BD=1��
��Rt��ABD��AD=$\sqrt{A{B}^{2}+B{D}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$��
��AF=DF��
��BF=$\frac{1}{2}$AD=$\frac{\sqrt{10}}{2}$��
��2��֤������ͼ2�У��ӳ�EF��N��ʹ��FN=EF������BN���ӳ�DE��AB��M��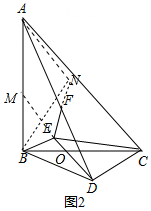
�ڡ�AFN�͡�DFE�У�
$\left\{\begin{array}{l}{AF=DF}\\{��AFN=��DFE}\\{FN=EF}\end{array}\right.$��
���AFN�ա�DFE��
��AN=DE=DC����FAN=��FDE��
��DM��AN��
���OMB=��BAN��
�ߡ�MOB+��OMB=90�㣬��DOC+��COD=90�㣬
�ߡ�MOB=��DOC��
���OMB=��OCD��
���BAN=��BCD��
�ڡ�BAN�͡�BCD�У�
$\left\{\begin{array}{l}{BA=BC}\\{��BAN=��BCD}\\{AN=CD}\end{array}\right.$��
���BAN�ա�BCD��
���ABN=��CBD��BN=BD��
���DBN=��CBA=90�㣬
�ߡ�DBE=45�㣬
���EBN=��EBD����BE=BE��BN=BD��
���BEN�ա�BED��
��DE=EN=2EF��
��3����ͼ3�У�����AE���ӳ�CD��AB��M����BC��ȡһ��N��ʹ��NM=NC����BM=m��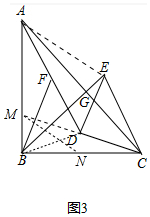
�ߡ�ACD=30�㣬��BCA=��DCE=45�㣬
���BCD=��ACE=15�㣬
�ߵ�E���߶�AC�Ĵ�ֱƽ�����ϣ�
��EA=EC��
���EAC=��ECA=15�㣬
��$\frac{AC}{BC}$=$\frac{EC}{CD}$=$\sqrt{2}$��
���BCD�ס�ACE��
���DBC=��EAC=15�㣬
���DBC=��DCB=15�㣬
��DB=DC��
���DBM=��DMB=75�㣬
��DM=DB=DC��
��Rt��MNB�У���BM=m����MNB=30�㣬
��NM=CN=2m��BN=$\sqrt{3}$m��
��CM=$\sqrt{B{M}^{2}+B{C}^{2}}$=$\sqrt{{m}^{2}+��\sqrt{3}m+2m��^{2}}$=��$\sqrt{2}$+$\sqrt{6}$��m��
��BD=$\frac{\sqrt{2}+\sqrt{6}}{2}$m��
��BD2=��2+$\sqrt{3}$��m2��
��BM•BA=BM•BC=m��2m+$\sqrt{3}$m��=��2+$\sqrt{3}$��m2��
��BD2=BM•BA��
��$\frac{BD}{AB}$=$\frac{BM}{BD}$���ߡ�DBM=��ABD��
���DBM�ס�ABD��
���BAD=��BDM=30�㣬
���ABD=��ADB=75�㣬
��AB=AD��
Ϊ�˿�����ѡ�ABD�Ƶ���ͼ4����BH��AD��H����BH��ȡһ��G��ʹ��BG=DG����DH=a��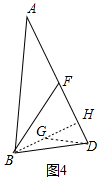
��BG=DG=2a��GH=$\sqrt{3}$a��BD=��$\sqrt{2}$+$\sqrt{6}$��a��
��Rt��ABH�У��ߡ�A=30�㣬
��AB=AD=2BH=��4+2$\sqrt{3}$��a��
��AF=DF=��2+$\sqrt{3}$��a��
��FH=��1+$\sqrt{3}$��a��
��Rt��BFH��BF=$\sqrt{F{H}^{2}+B{H}^{2}}$=$\sqrt{��1+\sqrt{3}��^{2}{a}^{2}+��2+\sqrt{3}��^{2}{a}^{2}}$��
��BF2=��11+6$\sqrt{3}$��a2��CD2=BD2=��8+4$\sqrt{3}$��a2��
�ࣨ$\frac{BF}{CD}$��2=$\frac{11+6\sqrt{3}}{8+4\sqrt{3}}$=$\frac{4+\sqrt{3}}{4}$��
���� ���⿼���������ۺ��⣬ȫ�������ε��ж������ʣ����������ε��ж������ʡ����ɶ�������ֱ�������ε����ʡ�ֱ��������б�����ߵ����ʵ�֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ�����ȫ�������λ����������ν�����⣬ѧ�����ò���������⣬�������������ν�ϵ�˼�룬�����������ͻ�Ƶ���֤��AB=AB����BAD=30�㣬��Ŀ�Ƚ��ѣ������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
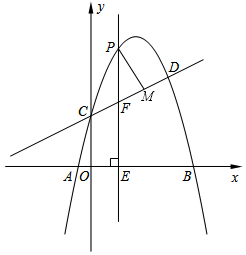 ��ͼ��������y=-x2+bx+c��ֱ��y=x+4����C��D���㣬���е�C��y���ϣ���D������Ϊ��6��7������P��y���Ҳ����������һ���㣬����P��PE��x���ڵ�E����CD�ڵ�F����PM��CD�ڵ�M��
��ͼ��������y=-x2+bx+c��ֱ��y=x+4����C��D���㣬���е�C��y���ϣ���D������Ϊ��6��7������P��y���Ҳ����������һ���㣬����P��PE��x���ڵ�E����CD�ڵ�F����PM��CD�ڵ�M���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ֱ������ϵxOy�У���ABC��������������ֱ�ΪA��-4��1����B��-1��1����C��-4��3����
��ͼ����ֱ������ϵxOy�У���ABC��������������ֱ�ΪA��-4��1����B��-1��1����C��-4��3�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 23��ʾ2��3�Ļ� | |
| B�� | �κ�һ����������ż�η������� | |
| C�� | һ������ƽ����$\frac{4}{9}$�������һ����$\frac{2}{3}$ | |
| D�� | -32�루-3��2��Ϊ�෴�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com