
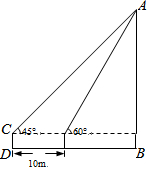
 如图,为了测得一棵树的高度AB,小明在D处用高为1m的测角仪CD,测得树顶A的仰角为45°,再向树方向前进10m,又测得树顶A的仰角为60°,求这棵树的高度AB.
如图,为了测得一棵树的高度AB,小明在D处用高为1m的测角仪CD,测得树顶A的仰角为45°,再向树方向前进10m,又测得树顶A的仰角为60°,求这棵树的高度AB. 分析 设AG=x,分别在Rt△AFG和Rt△ACG中,表示出CG和GF的长度,然后根据DE=10m,列出方程即可解决问题.
解答 解:设AG=x.
在Rt△AFG中,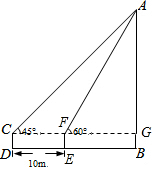
∵tan∠AFG=$\frac{AG}{FG}$,
∴FG=$\frac{x}{\sqrt{3}}$,
在Rt△ACG中,∵∠GCA=45°,
∴CG=AG=x,
∵DE=10,
∴x-$\frac{x}{\sqrt{3}}$=10,
解得:x=15+5$\sqrt{3}$
∴AB=15+5$\sqrt{3}$+1=16+5$\sqrt{3}$(米).
答:这棵树的高度AB为(16+5$\sqrt{3}$)米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:解答题
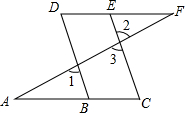 完成下列推理过程
完成下列推理过程查看答案和解析>>
科目:初中数学 来源: 题型:解答题
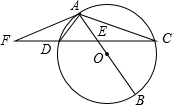 如图,已知AB是⊙O的直径,弦CD交AB于点E,作∠DAF=∠ACD,交CD延长线于点F.
如图,已知AB是⊙O的直径,弦CD交AB于点E,作∠DAF=∠ACD,交CD延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com