
【题目】如图,在△ABC中,AB=AC,点D在△ABC内,BD=BC,∠DBC=60°,点E在△ABC外,∠BCE=150°,∠ABE=60°.
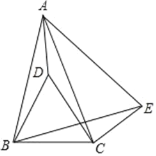
(1)求证:△ADB≌△ADC , 并求出∠ADB的度数;
(2)小明说△ABE是等腰三角形,小华说△ABE是等边三角形.请问 说法更准确,并说明理由.
(3)连接DE,若DE⊥BD,DE=8,求AD的长.
【答案】(1)150°;(2) 小华更准确,理由详见解析;(3)4
【解析】
(1)首先证明△DBC是等边三角形,推出∠BDC=60°,可证明△ADB≌△ADC,继而推出∠ADB=∠ADC即可解决问题;
(2)小华更准确,△ABE是等边三角形.只要证明△ABD≌△EBC即可.
(3)首先证明△DEC是含有30度角的直角三角形,求出EC的长,理由全等三角形的性质即可解决问题.
(1)∵BD=BC,∠DBC=60° ,
∴△DBC是等边三角形 ,
∴DB=DC,∠BDC=∠DBC=∠DCB=60°
在△ADB和△ADC中, 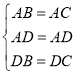 ,
,
∴△ADB≌△ADC(SSS),
∴∠ADB=∠ADC
∴∠ADB=![]() (360°﹣60°)=150°
(360°﹣60°)=150°
(2)解:结论:小华更准确,
理由:
∵∠ABE=∠DBC=60°,
∴∠ABD=∠CBE ,
在△ABD和△EBC中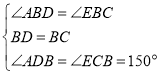 ,
,
∴△ABD≌△EBC(ASA),
∴AB=BE ,
∵∠ABE=60° ,
∴△ABE是等边三角形.
(3)连接DE,
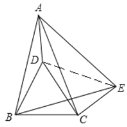
∵∠BCE=150°,∠DCB=60° ,
∴∠DCE=90°,
∵∠EDB=90°,∠BDC=60° ,
∴∠ED=30° ,
∴![]() ,
,
∵△ABD≌△EBC,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(2,8),且与x轴相切于点B.
(1)当x>0,y=5时,求x的值;
(2)当x = 6时,求⊙P的半径;
(3)求y关于x的函数表达式,请判断此函数图象的形状,并在图②中画出此函数的图象(不必列表,画草图即可).


图① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
①4a+c<0;②m(am+b)+b>a(m≠﹣1);③关于x的一元二次方程ax2+(b﹣1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是( )
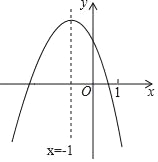
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,牧童家在B处,A、B两处相距河岸的距离AC、BD分别为500m和300m,且C、D两处的距离为600m,天黑牧童从A处将牛牵到河边去饮水,在赶回家,那么牧童最少要走( )
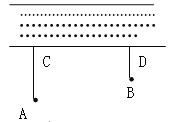
A.800mB.1000mC.1200mD.1500m
查看答案和解析>>
科目:初中数学 来源: 题型:
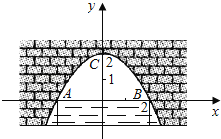
【题目】图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
(1)求拱桥所在抛物线的解析式;
(2)当水面下降1m时,则水面的宽度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为支援灾区建设,计划向![]() 、
、![]() 两受灾地运送急需物资分别为60吨和140吨,该市甲、乙两地有急需物资分别为120吨和80吨,已知甲、乙两地运到
两受灾地运送急需物资分别为60吨和140吨,该市甲、乙两地有急需物资分别为120吨和80吨,已知甲、乙两地运到![]() 、
、![]() 两地的每吨物资的运费如表所示:
两地的每吨物资的运费如表所示:
甲 | 乙 | |
| 20元/吨 | 15元/吨 |
| 25元/吨 | 24元/吨 |
(1)设甲地运到![]() 地的急需物资为
地的急需物资为![]() 吨,求总运费
吨,求总运费![]() (元)关于
(元)关于![]() (吨)的函数关系式,并写出
(吨)的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)求最低总运费,并说明总运费最低时的运送方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题背景)如图1所示,在![]() 中,
中,![]() ,
,![]() ,点D为直线
,点D为直线![]() 上的个动点(不与B、C重合),连结
上的个动点(不与B、C重合),连结![]() ,将线段
,将线段![]() 绕点D按顺时针方向旋转90°,使点A旋转到点E,连结
绕点D按顺时针方向旋转90°,使点A旋转到点E,连结![]() .
.
(问题初探)如果点D在线段![]() 上运动,通过观察、交流,小明形成了以下的解题思路:过点E作
上运动,通过观察、交流,小明形成了以下的解题思路:过点E作![]() 交直线
交直线![]() 于F,如图2所示,通过证明
于F,如图2所示,通过证明![]() ______,可推证
______,可推证![]() 是_____三角形,从而求得
是_____三角形,从而求得![]() ______°.
______°.
(继续探究)如果点D在线段![]() 的延长线上运动,如图3所示,求出
的延长线上运动,如图3所示,求出![]() 的度数.
的度数.
(拓展延伸)连接![]() ,当点D在直线
,当点D在直线![]() 上运动时,若
上运动时,若![]() ,请直接写出
,请直接写出![]() 的最小值.
的最小值.
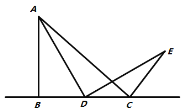
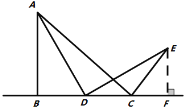
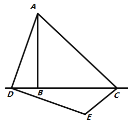
图1 图2 图3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com