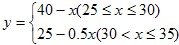Question

为推进节能减排，发展低碳经济，深化“宜居重庆”的建设，我市某“用电大户”用480万元购得“变频调速技术”后，进一步投入资金1520万元购买配套设备，以提高用电效率达到节约用电的目的．已知该“用电大户”生产的产品“草甘磷”每件成本费为40元．经过市场调研发现：该产品的销售单价，需定在100元到300元之间较为合理．当销售单价定为100元时，年销售量为20万件；当销售单价超过100元，但不超过200元时，每件新产品的销售价格每增加10元，年销售量将减少0.8万件；当销售单价超过200元，但不超过300元时，每件产品的销售价格在200元的基础上每增加10元，年销售量将减少1万件．设销售单价为x元），年销售量为y万件），年获利为w万元）．
（年获利=年销售额-生产成本-节电投资）
（1）直接写出y与x间的函数关系式；
（2）求第一年的年获利w与x函数关系式，并说明投资的第一年，该“用电大户”是盈利还是亏损？若盈利，最大利润是多少？若亏损，最少亏损是多少？
（3）若该“用电大户”把“草甘磷”的销售单价定在超过100元，但不超过200元的范围内，并希望到第二年底，除去第一年的最大盈利（或最小亏损）后，两年的总盈利为1842万元，请你确定此时销售单价．在此情况下，要使产品销售量最大，销售单价应定为多少元？

Answer 1

分析：（1）分段讨论当100＜x≤200和当200＜x≤300的函数关系式，
（2）由年获利=年销售额-生产成本-节电投资分别列出当100＜x≤200和200＜x≤300的利润关系式，求出最大利润，
（3）依题意可知，当100＜x≤200时，写出第二年w与x关系为式，由两年的总盈利为1842万元，解得单价x．

解答：解：（1）当100＜x≤200，
y=20-

x-100

10

×0.8，
∴y=-

2

25

x+28，
当200＜x≤300，
把x=200代入y=-

2

25

x+28，
得：y=12，
∴y=12-

x-200

10

×1，
y=-

1

10

x+32；

（2）当100＜x≤200时，
w=（x-40）y-（1520+480）
=(x-40)(-

2

25

x+28)-2000，
=-

2

25

x2+

156

5

x-3120，
=-

2

25

(x-195)2-78
∵-

2

25

＜0
x=195，w_最大=-78
当200＜x≤300时，
w=（x-40）y-（1520+480）
=(x-40)(-

1

10

x+32)-2000，
=-

1

10

x2+36x-3280，
=-

1

10

(x-180)2-40，
当x=180时，不在200＜x≤300范围内，
∵-

2

25

＜0，∴当在200＜x≤300时，y随x的增大而减小，
∴w＜-80
是亏损的，最少亏损为78万元．（7分）

（3）依题意可知，当100＜x≤200时，第二年w与x关系为
w=(x-40)(-

2

25

x+28)-78
当总利润刚好为1842万元时，依题意可得(x-40)(-

2

25

x+28)-78=1842（8分）
整理，得x²-390x+38000=0
解得，x₁=190，x₂=200
∴要使两年的总盈利为1842万元，销售单价可定为190元或200元．（9分）
∵对y=-

2

25

x+28，y随x增大而减小
∴使销售量最大的销售单价应定为190元．（10分）

点评：本题主要考查二次函数的应用，用二次函数解决实际问题，比较简单．