
【题目】为了倡导绿色出行,某市政府2016年投资了320万元,首期建成120个公共自行车站点,配置2500辆公共自行车,2017年又投资了104万元新建了40个公共自行车站点,配置800辆公共自行车.
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)若到2020年该市政府将再建造![]() 个新公共自行车站点和配置
个新公共自行车站点和配置![]() 辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?(注:从2016年起至2020年,每个站点的造价和公共自行车的单价每年都保持不变)
辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?(注:从2016年起至2020年,每个站点的造价和公共自行车的单价每年都保持不变)
【答案】(1)每个站点的造价1万元,公共自行车的单价0.08万元;
(2)市政府共有3种选择方案,第一种方案市政府投入的资金最,资金为284万元.
【解析】试题分析:(1)设每个站点的造价![]() 万元,公共自行车的单价
万元,公共自行车的单价![]() 万元,根据题意列出方程组求出即可;
万元,根据题意列出方程组求出即可;
(2)根据题意列出不等式组即可得.
试题解析:(1)设每个站点的造价![]() 万元,公共自行车的单价
万元,公共自行车的单价![]() 万元,
万元,
根据题意,得![]() ,
,
解这个方程组,得![]() ,
,
答:每个站点的造价1万元,公共自行车的单价0.08万元.
(2)根据题意可得![]() ,解得
,解得![]() ,
,
∵![]() 为整数,
为整数,
∴![]() =100或
=100或![]() =101或
=101或![]() =102,
=102,
∴共有3种方案:
第一种方案:建造100个新公共自行车站点,配置2300辆公共自行车;资金为:![]() (万元)
(万元)
第二种方案:建造101个新公共自行车站点,配置2299辆公共自行车;资金为:![]() (万元)
(万元)
第三种方案:建造102个新公共自行车站点,配置2298辆公共自行车;资金为:![]() (万元)
(万元)
∴第一种方案市政府投入的资金最少 ,
答:市政府共有3种选择方案,第一种方案市政府投入的资金最,资金为284万元.


科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2=180°,∠DAE=∠BCF.
(1)试判断直线AE与CF有怎样的位置关系?并说明理由;
(2)若∠BCF=70°,求∠ADF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上.
(1)求证:AE2+AD2=2AC2;
(2)如图2,若AE=3,AC=![]() ,点F是AD的中点,求出CF的长.
,点F是AD的中点,求出CF的长.
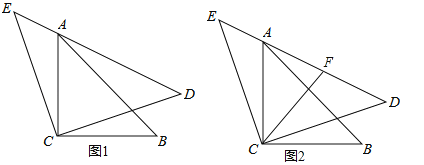
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)将一张长方形纸片按如图1所示的方式折叠,BC、BD为折痕,求∠CBD的度数;
(2)将一张长方形纸片按如图2所示的方式折叠,BC、BD为折痕,若∠A′BE′=50°,求∠CBD的度数;
(3)将一张长方形纸片按如图3所示的方式折叠,BC、BD为折痕,若∠A′BE′=α,请直接写出∠CBD的度数(用含α的式子表示)
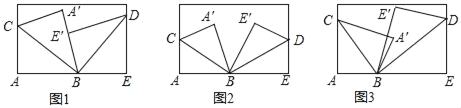
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:
已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
小明发现,可以设另一个因式为(x+n),得
x2﹣4x+m=(x+3)(x+n)
则x2﹣4x+m=x2+(n+3)x+3n
∴![]()
利用方程组可以解决.
请回答:
另一个因式为 ,m的值为 ;
参考小明的方法,解决下面的问题:
已知二次三项式2x2+3x﹣k有一个因式是(x﹣4),求另一个因式以及k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是中华民族古老的传统节日.甲、乙两家超市在“端午节”当天对一种原来售价相同的粽子分别推出了不同的优惠方案.
甲超市方案:购买该种粽子超过200元后,超出200元的部分按95%收费;
乙超市方案:购买该种粽子超过300元后,超出300元的部分按90%收费.
设某位顾客购买了x元的该种粽子.
(1)补充表格,填写在“横线”上:
(2)列式计算说明,如果顾客在“端午节”当天购买该种粽子超过200元,那么到哪家超市花费更少?
x (单位:元) | 实际在甲超市的花费 (单位:元) | 实际在乙超市的花费 (单位:元) |
0<x≤200 | x | x |
200<x≤300 | x | |
x>300 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC, D为直线BC上一动点(不与B,C重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
(1)当D在线段BC上时,求证:△BAD ≌△CAE;
(2)当点D运动到何处时,AC⊥DE,并说明理由;
(3)当CE∥AB时,若△ABD中最小角为20°,直接写出∠ADB的度数.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com