
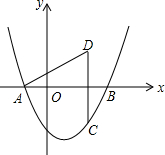
 如图,抛物线为y=$\frac{\sqrt{3}}{3}$(x+1)(x-3)x轴交于A、B两点(点A在点B左侧),
如图,抛物线为y=$\frac{\sqrt{3}}{3}$(x+1)(x-3)x轴交于A、B两点(点A在点B左侧),分析 (1)将点C的坐标代入抛物线的解析式即可求得m的值;
(2)令y=0可求得点A的坐标,由抛物线的对称性可得到点D的坐标,然后根据平行四边形的定义画出图形,接下来,依据平行四边形对边平行且相等的性质可求得定E的坐标;
(3)记DC与x轴的交点为M,连接PM.依据S=S△AMD+S△PAM+SCPM得到S与a的函数关系式,接下来,依据二次函数的性质可求得S的最大值;
(4)如图5所示:以AD为直径作圆F,直线$y=\frac{{\sqrt{3}}}{3}x+m$与圆F的交点Q满足∠AQD=90°(Q与A、D不重合).过点H作HM⊥直线y=$\frac{\sqrt{3}}{3}$x+m,垂足为M.先求得直线AD的解析式,从而可知直线AD与直线y=$\frac{\sqrt{3}}{3}$x+m平行,在△MGH中依据特殊锐角三角函数值可求得HG的长度,从而得到点G和点G′的坐标,从而得到m的取值范围.
解答 解:(1)∵将x=2,代入抛物线的解析式得;y=$\frac{\sqrt{3}}{3}$×3×(-1)=-$\sqrt{3}$,
∴m=-$\sqrt{3}$.
故答案为;-$\sqrt{3}$.
(2)∵点C与点D关于x轴对称,点C(2,-$\sqrt{3}$),
∴DC=2$\sqrt{3}$.
令y=0,得$\frac{\sqrt{3}}{3}$(x+1)(x-3)=0.
解得:x1=-1,x2=3,
∴A(-1,0),B(3,0).
如图1所示;
∵ADCE为平行四边形,
∴AE=DC.
∴AE=2$\sqrt{3}$.
∴E(-1,-2$\sqrt{3}$).
如图2所示:
∵ADCE为平行四边形,
∴AE=DC.
∴AE=2$\sqrt{3}$.
∴E(-1,2$\sqrt{3}$).
如图3所示;
∵ACED为平行四边形,
∴AF=EF.
又∵AE⊥DC,
∴点E与点A关于CD对称.
∴AE=6.
∴OE=5
∴E(5,0).
综上所述点E的坐标为(5,0),(-1,2$\sqrt{3}$),(-1,-2$\sqrt{3}$).
(3)如图4:记DC与x轴的交点为M,连接PM.
设点p的坐标为(a,$\frac{\sqrt{3}}{3}$a2-$\frac{2\sqrt{3}}{3}$a-$\sqrt{3}$).
∵S△AMD=$\frac{1}{2}$AM•MD=$\frac{1}{2}$×$\sqrt{3}$×3=$\frac{3\sqrt{3}}{2}$,S△PAM=$\frac{1}{2}$AM•|$\frac{\sqrt{3}}{3}$a2-$\frac{2\sqrt{3}}{3}$a-$\sqrt{3}$|=-$\frac{\sqrt{3}}{2}$a2+$\sqrt{3}$a+$\frac{3\sqrt{3}}{2}$,S△PMC=$\frac{1}{2}$MC•PC=$\sqrt{3}$-$\frac{\sqrt{3}}{2}$a,
∴S=S△AMD+S△PAM+SCPM=$-\frac{\sqrt{3}}{2}$a2+$\frac{\sqrt{3}}{2}$a$+4\sqrt{3}$.
∴S=$-\frac{\sqrt{3}}{2}$(a-$\frac{1}{2}$)2+$\frac{33\sqrt{3}}{8}$.
∵-$\frac{\sqrt{3}}{2}$<0,
∴当a=$\frac{1}{2}$时,S取得最大值,S的最大值是$\frac{{33\sqrt{3}}}{8}$.
(4)如图5所示:以AD为直径作圆F,直线$y=\frac{{\sqrt{3}}}{3}x+m$与圆F的交点Q满足∠AQD=90°(Q与A、D不重合).过点H作HM⊥直线y=$\frac{\sqrt{3}}{3}$x+m,垂足为M.
∵由两点间的距离公式可知:AD=2$\sqrt{3}$,
∴圆F的半径为$\sqrt{3}$.
设直线AD的解析式为y=kx+b.
将点A和点D的坐标代入得:$\left\{\begin{array}{l}{-k+b=0}\\{2k+b=\sqrt{3}}\end{array}\right.$,
解得:k=$\frac{\sqrt{3}}{3}$,b=$\frac{\sqrt{3}}{3}$.
∴直线AD与直线y=$\frac{\sqrt{3}}{3}$x+m平行.
当直线$y=\frac{{\sqrt{3}}}{3}x+m$与圆相切时,MH=FQ=$\sqrt{3}$.
当Q在AD的上方时,在△HMG中,HG=MH÷$\frac{\sqrt{3}}{2}$=2.
∴OG=2+$\frac{\sqrt{3}}{3}$.
当点Q在AD的下方时,HG′=2,
∴OG′=2$-\frac{\sqrt{3}}{3}$.
∴m的取值范围是:$\frac{{\sqrt{3}}}{3}-2≤$m≤$\frac{{\sqrt{3}}}{3}+2$,且$m≠\frac{{\sqrt{3}}}{3}$.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式、函数图象与坐标轴的交点、平行四边形的性质、特殊锐角三角函数值,根据题意得到S与a的函数关系式以及求得OG和OG′的长度是解题的关键.


科目:初中数学 来源: 题型:选择题
 如图,AB是半圆的直径,点D是$\widehat{AC}$的中点,∠ABC=50°,则∠DAB等于( )
如图,AB是半圆的直径,点D是$\widehat{AC}$的中点,∠ABC=50°,则∠DAB等于( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图AB是⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
如图AB是⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com