
分析 (1)根据绝对值、幂的乘方、零指数幂可以解答本题;
(2)根据分式的减法和除法可以解答本题.
解答 解:(1)|1-$\sqrt{3}$|+(-1)2017-(3-π)0
=$\sqrt{3}-1+(-1)-1$
=$\sqrt{3}-3$;
(2)(1-$\frac{1}{x-1}$)÷$\frac{x-2}{x-{x}^{2}}$
=$\frac{x-1-1}{x-1}×\frac{x(1-x)}{x-2}$
=$\frac{x-2}{x-1}×\frac{x(1-x)}{x-2}$
=-x.
点评 本题考查分式的混合运算、实数的运算、零指数幂,解答本题的关键是明确它们各自的计算方法.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:选择题
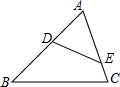 在△ABC与△AED中,$\frac{AE}{AB}$=$\frac{AD}{AC}$=$\frac{1}{2}$,则S△ADE:S△ABC的值为( )
在△ABC与△AED中,$\frac{AE}{AB}$=$\frac{AD}{AC}$=$\frac{1}{2}$,则S△ADE:S△ABC的值为( )| A. | $1:\sqrt{3}$ | B. | 1:2 | C. | 1:3 | D. | 1:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
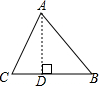 如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购进甲种服装的数量/件 | 10 | 20 | x |
| 购进甲种服装所用费用/元 | 800 | 1600 | 80x |
| 购进乙种服装所用费用/元 | 5400 | 4800 | 6000-60x |
| 购进甲种服装的数量/件 | 10 | 20 | x |
| 甲种服装获得的利润/元 | 400 | 800 | 40x |
| 乙种服装获得的利润/元 | 2700 | 2400 | 3000-30x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
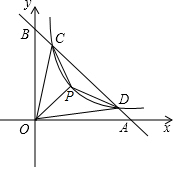 如图,已知C,D是反比例函数y=$\frac{m}{x}$图象在第一象限内的分支上的两点,直线CD分别交x轴,y轴于A,B两点,设C,D的坐标分别是(x1,y1),(x2,y2),连结OC,OD.
如图,已知C,D是反比例函数y=$\frac{m}{x}$图象在第一象限内的分支上的两点,直线CD分别交x轴,y轴于A,B两点,设C,D的坐标分别是(x1,y1),(x2,y2),连结OC,OD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
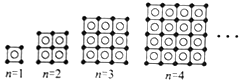 下列各个图形中,“•”的个数用a表示,“○”的个数用b表示,如:n=1时,a=4,b=1;n=2时,a=9,b=4;…根据图形的变化规律,当n=2017时,$\sqrt{a}$+$\sqrt{b}$的值为4035.
下列各个图形中,“•”的个数用a表示,“○”的个数用b表示,如:n=1时,a=4,b=1;n=2时,a=9,b=4;…根据图形的变化规律,当n=2017时,$\sqrt{a}$+$\sqrt{b}$的值为4035.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com