
【题目】已知直线AB和CD交于点O,∠AOC的度数为x,∠BOE=90°,OF平分∠AOD.
(1)当x=19°48′,求∠EOC与∠FOD的度数.
(2)当x=60°,射线OE、OF分别以10°/s,4°/s的速度同时绕点O顺时针转动,求当射线OE与射线OF重合时至少需要多少时间?
(3)当x=60°,射线OE以10°/s的速度绕点O顺时针转动,同时射线OF也以4°/s的速度绕点O逆时针转动,当射线OE转动一周时射线OF也停止转动.射线OE在转动一周的过程中当∠EOF=90°时,求射线OE转动的时间.

【答案】(1)∠EOC=70°12′,∠FOD=80°6′;(2)射线OE与射线OF重合时至少需要35秒;(3)射线OE转动的时间为t=![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用互余和互补的定义可得:∠EOC与∠FOD的度数.
(2)先根据x=60°,求∠EOF=150°,则射线OE、OF第一次重合时,则OE运动的度数-OF运动的度数=360-150,列式解出即可;
(3)分三种情况:①OE不经过OF时,②OE经过OF,但OF在OB的下方时;③OF在OB的上方时;根据其夹角列方程可得时间.
(1)∵∠BOE=90°,
∴∠AOE=90°,
∵∠AOC=x=19°48′,
∴∠EOC=90°-19°48′=89°60°-19°48′=70°12′,
∠AOD=180°-19°48′=160°12′,
∵OF平分∠AOD,
∴∠FOD=![]() ∠AOD=
∠AOD=![]() ×160°12′=80°6′;
×160°12′=80°6′;
(2)当x=60°,∠EOF=90°+60°=150°
设当射线OE与射线OF重合时至少需要t秒,
10t-4t=360-150,
t=35,
答:当射线OE与射线OF重合时至少需要35秒;
(3)设射线OE转动的时间为t秒,
分三种情况:①OE不经过OF时,得10t+90+4t=360-150,
解得,t=![]() ;
;
②OE经过OF,但OF在OB的下方时,得10t-(360-150)+4t=90
解得,t=![]() ;
;
③OF在OB的上方时,得:360-10t=4t-120
解得,t=![]() .
.
所以,射线OE转动的时间为t=![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】若a、b、c是正数,下列各式,从左到右的变形不能用如图验证的是( )
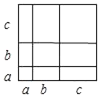
A. (b+c)2=b2+2bc+c2
B. a(b+c)=ab+ac
C. (a+b+c)2=a2+b2+c2+2ab+2bc+2ac
D. a2+2ab=a(a+2b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:
① ∠AOE=65°;② OF平分∠BOD;③ ∠GOE=∠DOF;④ ∠AOE=∠GOD,其中正确结论的个数是( )

A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2-2ax+a+4(a<0)经过点B.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.
①写出点M′的坐标;
②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设⊙B, ⊙M′都与直线l′相切,半径分别为R1、R2 , 当R1+R2最大时,求直线l′旋转的角度(即∠BAC的度数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )

A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c(a<0)的图象如图所示,且关于x的方程ax2+bx+c=k有两个不相等的实根,则常数k的取值范围是( )
A.0<k<4
B.﹣3<k<1
C.k<﹣3或k>1
D.k<4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了丰富学生的校园生活,准备购进一批篮球和足球.其中篮球的单价比足球的单价多40元,用1500元购进的篮球个数与900元购进的足球个数相等.
(1)篮球和足球的单价各是多少元?
(2)该校打算用1000元购买篮球和足球,问恰好用完1000元,并且篮球、足球都买有的购买方案有哪几种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题,如图,正方形ABCD。
(1)请在图①中作两条直线,使它们将正方形ABCD的面积三等分;
(2)如图②,在矩形ABCD中,AB=6,BC=9,在图②中过顶点A作两条直线,使它们将矩形ABCD的面积三等分,井说明理由;
(3)如图③,农博园有一块不规则的五边形ABCDE空地,其中AB∥CD、AE∥BC,AB=AC=100米,AE=160米,BC=120米,CD=62.5米,根据视觉效果和花期特点,农博园设计部门想在这片空地种上等面积的三种不同的花,要求从入口A点处修两条笔直的小路(小路的面积忽略不计)方便游客赏花,两条小路将这块地面积三等分.请通过计算画图说明其设计部们能否实现,若能实现请确定小路尽头的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)求出线段AB,曲线CD的解析式,并写出自变量的取值范围;
(2)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com