
分析 首先求得分式方程的解,然后根据方程的解为整数可求得k的值.
解答 解:去分母得:k(x-1)+3(x+1)=7.
去括号得:kx-k+3x+3=7.
解得:x=$\frac{4+k}{k+3}$.
∵$\frac{4+k}{k+3}$=1$+\frac{1}{k+3}$,且方程有整数解,
∴$\frac{1}{k+3}$=±1.
解得:k1=-2,k2=-4.
∴x1=0,x2=2.
经检验:x1=0,x2=2都是原方程的解.
故答案为:-2或-4.
点评 本题主要考查的是解分式方程、分式方程的解,根据求得x=1+$\frac{1}{k+3}$,然后方程的解为整数得到k的值是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
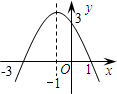 二次函数y=-x2-2x+3的图象如图所示,当y<0时,自变量x的取值范围是( )
二次函数y=-x2-2x+3的图象如图所示,当y<0时,自变量x的取值范围是( )| A. | -3<x<1 | B. | x<-3 | C. | x>1 | D. | x<-3或x>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,有一个二级台阶,每一级的长、宽、高分别为60cm,45cm,27cm,A和B是这两个台阶的相对端点,A点上有一只蚂蚁想到B点去吃可口的食物,若蚂蚁平均每秒走0.8cm,则蚂蚁沿着台阶从A到B至少需要多少时间?
如图所示,有一个二级台阶,每一级的长、宽、高分别为60cm,45cm,27cm,A和B是这两个台阶的相对端点,A点上有一只蚂蚁想到B点去吃可口的食物,若蚂蚁平均每秒走0.8cm,则蚂蚁沿着台阶从A到B至少需要多少时间?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com