
【题目】如图,已知在△ABC中,∠A=90
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明).
(2)若∠B=60,AB=3,求⊙P的面积.
科目:初中数学 来源: 题型:
【题目】在一个长为8分米,宽为5分米,高为7分米的长方体上,截去一个长为6分米,宽为5分米,深为2分米的长方体后,得到一个如图所示的几何体.一只蚂蚁要从该几何体的顶点A处,沿着几何体的表面到几何体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是 分米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给x人.
(1)求第一轮后患病的人数;(用含x的代数式表示)
(2)在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否会有21人患病的情况发生,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第________秒时,边CD恰好与边AB平行.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠A=60°,BD、BE三等分∠ABC,CD、CE三等分∠ACB,连接DE,则∠BDE=_____________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了选择1名车工参加加工直径为10 mm的精密零件的技术比赛,随机抽取甲、乙两名车工加工的5个零件,现测得的结果如下表,请你比较![]() 、
、![]() 的大小( )
的大小( )

A. ![]() >
>![]()
B. ![]() =
=![]()
C. ![]() <
<![]()
D. ![]() ≤
≤![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1 , 此时AP1= ![]() ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+ ![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+ ![]() ;…,按此规律继续旋转,直至得到点P2015为止.则AP2015= .
;…,按此规律继续旋转,直至得到点P2015为止.则AP2015= . 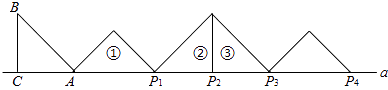
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芳芳同学手中有一块长方形纸板和一块正方形纸板,其中长方形纸板的长为3 dm,宽为2 dm,且两块纸板的面积相等.
(1)求正方形纸板的边长(结果保留根号).
(2)芳芳能否在长方形纸板上截出两个完整的,且面积分别为2 dm2和3 dm2的正方形纸板?判断并说明理由.(提示:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com