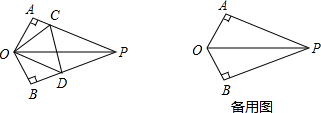
(1)证明:在Rt△AOP和Rt△BOP中,
∵
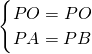
,
∴Rt△AOP≌Rt△BOP(HL);
(2)解:∵AC=a,BD=b,且a≠b,a与b满足a
2-10a+22=0,b
2-10b+22=0,
∴a,b是方程x
2-10x+22=0的两根,
∴a+b=AC+BD=10,
则AC+BD的值为10;
②∵AP=20,CD=10,AC+BD=10,
∴AC+BD=CD,
∴PC+CD+PD=PA+PB=20+20=40,
∴△PCD的周长=2AP,
故答案为:40,2.
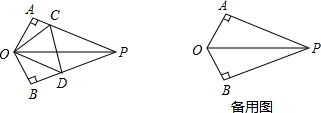
(3)证明:
延长射线PA到F使AF=BD,过O作OE⊥CD,
∵在△OAF和△OBD中,
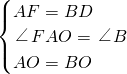
,
∴△OAF≌△OBD(SAS);
∴OF=OD;
∵△PCD的周长为=2AP,
∴△PCD的周长为=PA+PB=PC+PD+AC+BD=PC+PD+CD;
∴CD=AC+BD,
∵AF=BD,
∴CF=CD;
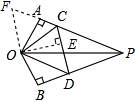
在△COF和△COD中,
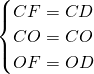
,
∴△OFC≌△OCD(SSS);
∴CF和CD边上所对应的高也应该相等.
∴OE=OA,
∵AO=BO,
∴BO=EO,
在Rt△OBD和Rt△OED中,

,
∴Rt△OBD≌Rt△OED(HL),
∴∠ODB=∠ODC,
即:OD平分∠BDC.
分析:(1)利用HL定理求出Rt△AOP≌Rt△BOP即可;
(2)①由已知得出a,b是方程x
2-10x+22=0的两根,再利用根与系数关系得出a+b=AC+BD=10即可;
②由CD=10,AC+BD=10,得出AC+BD=CD,进而求出PC+CD+PD=PA+PB得出答案即可,即可得出△PCD的周长=2AP;
(3)本题要充分利用△PCD周长=2AP的条件.延长射线PA到F,使AF=BD;易证得△OAF≌△OBD得OF=OD;由于△PCD周长=2AP,即l=PA+PB=PC+PD+CD,因此CD=AC+BD=AC+AF=CF;
再证明△OCF≌△OCD,那么两三角形的对应边上的高也相等,则OE=OA,然后再次证明Rt△OBD≌Rt△OED可得∠ODB=∠ODC.
点评:此题主要考查了全等三角形全等的判定与性质,是一个很好的开放题,关键是掌握证明三角形全等的判定方法SSS、SAS、AAS、ASA.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.

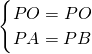 ,
,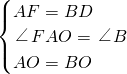 ,
,
 ,
, ,
,

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
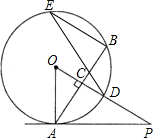 如图,PA与⊙O相切于A点,弦AB⊥OP,垂足为C,OP与⊙O相交于D点,E为圆周上一点,连接EB、ED,已知OA=2,OP=4.则∠BED的度数为
如图,PA与⊙O相切于A点,弦AB⊥OP,垂足为C,OP与⊙O相交于D点,E为圆周上一点,连接EB、ED,已知OA=2,OP=4.则∠BED的度数为 已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.
已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.