
 如图,在△ABC中,AB=BC=4,S△ABC=4$\sqrt{3}$,点P、Q、K分别为线段AB、BC、AC上任意一点,则PK+QK的最小值为2$\sqrt{3}$.
如图,在△ABC中,AB=BC=4,S△ABC=4$\sqrt{3}$,点P、Q、K分别为线段AB、BC、AC上任意一点,则PK+QK的最小值为2$\sqrt{3}$. 分析 根据轴对称确定最短路线问题,作点P关于BD的对称点P′,连接P′Q与BD的交点即为所求的点K,然后根据直线外一点到直线的所有连线中垂直线段最短的性质可知P′Q⊥BC时PK+QK的最小值,然后求解即可.
解答 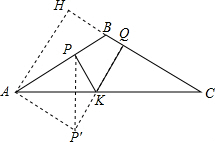 解:如图,过A作AH⊥BC交CB的延长线于H,
解:如图,过A作AH⊥BC交CB的延长线于H,
∵AB=CB=4,S△ABC=4$\sqrt{3}$,
∴AH=2$\sqrt{3}$,
∴cos∠HAB=$\frac{AH}{AB}=\frac{2\sqrt{3}}{4}$=$\frac{\sqrt{3}}{2}$,
∴∠HAB=30°,
∴∠ABH=60°,
∴∠ABC=120°,
∵∠BAC=∠C=30°,
作点P关于直线AC的对称点P′,
过P′作P′Q⊥BC于Q交AC于K,
则P′Q 的长度=PK+QK的最小值,
∴∠P′AK=∠BAC=30°,
∴∠HAP′=90°,
∴∠H=∠HAP′=∠P′QH=90°,
∴四边形AP′QH是矩形,
∴P′Q=AH=2$\sqrt{3}$,
即PK+QK的最小值为2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查了轴对称确定最短路线问题,矩形的性质,解直角三角形,熟记利用轴对称确定最短路线的方法是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 总体 | B. | 个体 | C. | 样本 | D. | 样本容量 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 购买一张福利彩票,中特等奖 | |
| B. | 在一个标准大气压下,加热水到100℃,沸腾 | |
| C. | 任意三角形的内角和为180° | |
| D. | 在一个仅装着白球和黑球的袋中摸出红球 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1,0) | B. | (1,-4) | C. | (-1,0) | D. | (-5,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
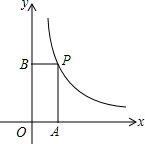 如图,在平面直角坐标系中,点P是反比例函数y=$\frac{k}{x}$(x>0)图象上的一点,分别过点P作PA⊥x轴于点A,PB⊥y轴于点B.若四边形OAPB的面积为3,则k的值为( )
如图,在平面直角坐标系中,点P是反比例函数y=$\frac{k}{x}$(x>0)图象上的一点,分别过点P作PA⊥x轴于点A,PB⊥y轴于点B.若四边形OAPB的面积为3,则k的值为( )| A. | 3 | B. | -3 | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com