
| k |
| x |
| k |
| x |
| x |
| x |
|
|
| k |
| x |
|
| k |
| k |
| x |
| k |
| x |
|
| k |
| 4800 |
| 3 |
| 1600 |
| x |
| 1600 |
| x |
| 9600 |
| x |
| 1152000 |
| x |
| k |
| x |
| k |
| x |
|
| k |
| 1152000 |
| x |
720x•
|


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:
| ab |
A、120
| ||
B、60
| ||
| C、120 | ||
| D、60 |
查看答案和解析>>
科目:初中数学 来源:2010年中考数学考前10日信息题复习题精选(4)(解析版) 题型:选择题
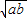 成立.某同学在做一个面积为3 600cm2,对角线相互垂直的四边形风筝时,运用上述规律,求得用来作对角线用的竹条至少需要准备xcm.则x的值是( )
成立.某同学在做一个面积为3 600cm2,对角线相互垂直的四边形风筝时,运用上述规律,求得用来作对角线用的竹条至少需要准备xcm.则x的值是( )
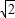
查看答案和解析>>
科目:初中数学 来源:2009年浙江省宁波市兴宁中学中考提前批招生考试数学试卷(解析版) 题型:选择题
 成立.某同学在做一个面积为3 600cm2,对角线相互垂直的四边形风筝时,运用上述规律,求得用来作对角线用的竹条至少需要准备xcm.则x的值是( )
成立.某同学在做一个面积为3 600cm2,对角线相互垂直的四边形风筝时,运用上述规律,求得用来作对角线用的竹条至少需要准备xcm.则x的值是( )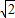

查看答案和解析>>
科目:初中数学 来源:2005年山东省日照市中考数学试卷(解析版) 题型:选择题
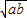 成立.某同学在做一个面积为3 600cm2,对角线相互垂直的四边形风筝时,运用上述规律,求得用来作对角线用的竹条至少需要准备xcm.则x的值是( )
成立.某同学在做一个面积为3 600cm2,对角线相互垂直的四边形风筝时,运用上述规律,求得用来作对角线用的竹条至少需要准备xcm.则x的值是( )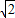

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com