
【题目】下列问题中,两个变量成反比例的是( )
A.长方形的周长确定,它的长与宽
B.长方形的长确定,它的周长与宽
C.长方形的面积确定,它的长与宽
D.长方形的长确定,它的面积与宽
【答案】C
【解析】
试题根据反比例函数的定义解答.例如:在本题中,长方形的面积=长×宽,即长和宽的乘积为定值,所以根据反比例的概念应该是长和宽成反比例;长方形的周长=2×(长+宽),即长和宽的和为定值,所以根据正比例的概念应该是长和宽成正比例.
解:A、长方形的周长=2×(长+宽),即长和宽的和为定值,所以根据正比例的概念应该是长和宽成正比例.故本选项错误;
B、长方形的周长=2×(长+宽),所以,长=![]() ﹣宽,即周长的一半长和宽的和为定值,所以根据正比例的概念应该是周长和宽成正比例.故本选项错误;
﹣宽,即周长的一半长和宽的和为定值,所以根据正比例的概念应该是周长和宽成正比例.故本选项错误;
C、长方形的面积=长×宽,即长和宽的乘积为定值,所以根据反比例的概念应该是长和宽成反比例;故本选项正确;
D、长方形的面积=长×宽,即长和宽的乘积为定值,所以根据正比例的概念应该是长和宽成正比例;故本选项错误;
故选C.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
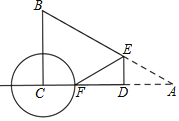
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4![]() .若动点D在线段AC上(不与点A、C重合),过点D作DE⊥AC交AB边于点E.点A关于点D的对称点为点F,以FC为半径作⊙C,当DE=_______时,⊙C与直线AB相切.
.若动点D在线段AC上(不与点A、C重合),过点D作DE⊥AC交AB边于点E.点A关于点D的对称点为点F,以FC为半径作⊙C,当DE=_______时,⊙C与直线AB相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:![]() ,则
,则![]() 是“和谐分式”.
是“和谐分式”.
(1)下列分式中,属于“和谐分式”的是_____(填序号);
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
(2)将“和谐分式”![]() 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为:![]() =_______(要写出变形过程);
=_______(要写出变形过程);
(3)应用:先化简![]() ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书“,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本书最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表,如图所示:
本数(本) | 频数(人数) | 频率 |
5 | a | 0.2 |
6 | 18 | 0.36 |
7 | 14 | b |
8 | 8 | 0.16 |
合计 | 50 | c |
我们定义频率=![]() ,比如由表中我们可以知道在这次随机调查中抽样人数为50人课外阅读量为6本的同学为18人,因此这个人数对应的频率就是
,比如由表中我们可以知道在这次随机调查中抽样人数为50人课外阅读量为6本的同学为18人,因此这个人数对应的频率就是![]() =0.36.
=0.36.
(1)统计表中的a、b、c的值;
(2)请将频数分布表直方图补充完整;
(3)求所有被调查学生课外阅读的平均本数;
(4)若该校八年级共有600名学生,你认为根据以上调查结果可以估算分析该校八年级学生课外阅读量为7本和8本的总人数为多少吗?请写出你的计算过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列说法不正确的是( )
(k≠0),下列说法不正确的是( )
A. 它的图象分布在第一、三象限 B. 点(k,k)在它的图象上
C. 它的图象关于原点对称 D. 在每个象限内y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
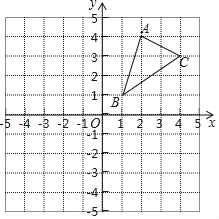
【题目】(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2.
(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,过点A作直线EF.
(1)如图①,AB是直径,要使EF是⊙O的切线,还须添加一个条件是(只需写出三种情况).
(ī) (īī) (īīī)
(2)如图(2),若AB为非直径的弦,∠CAE=∠B,则EF是⊙O的切线吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30千米/时,受影响区域的半径为200千米,B市位于点P的北偏东75°方向上,距离点P 320千米处.

(1) 说明本次台风会影响B市;
(2)求这次台风影响B市的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=16cm,AD=4cm,点P、Q分别从A、B同时出发,点P在边AB上沿AB方向以2cm/s的速度匀速运动,点Q在边BC上沿BC方向以1cm/s的速度匀速运动,当其中一点到达终点时,另一点也随之停止运动.设运动时间为x秒,△PBQ的面积为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.,并指出此时x的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com