
分析 根据题意,设外出到回家时针走了x°,则分针走了(2×110°+x°),可得到时针的度数,又因为时针每小时走30°,故外出用的时间可求.
解答 解:设时针从他外出到回家走了x°,则分针走了(2×110°+x°),由题意得
$\frac{220°+x°}{360°}$=$\frac{x°}{30°}$,
解得x=20°,
∵时针每小时走30°,
∴$\frac{20°}{30°}$=$\frac{2}{3}$小时,即外出用了40分钟时间.
解法2:设此人外出用了x分钟,则分针转了6x度,时针转了0.5x度,依题意得
6x-0.5x=110×2
解得x=40,
∴外出用了40分钟时间.
点评 本题考查钟表时针与分针的夹角.在钟表问题中,常利用时针与分针转动的度数关系:分针每转动1°时针转动($\frac{1}{12}$)°,并且利用起点时间时针和分针的位置关系建立数学模型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
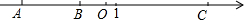 如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,CO=$\frac{5}{3}$AO.
如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,CO=$\frac{5}{3}$AO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-9+x2 | B. | y=-2x+1 | C. | y=$\sqrt{{x}^{2}+4}$ | D. | y=-(x+1)+3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com