
【题目】(1)问题发现
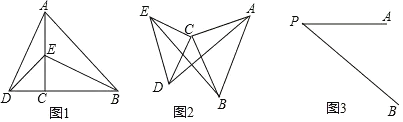
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上,填空:线段AD,BE之间的关系为
(2)拓展探究
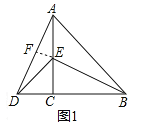
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.
(3)解决问题
如图3,线段PA=![]() ,点B是线段PA外一点,PB=3,连接AB绕点A逆时针旋转90°得到线段AC,随着点B的位置变化,直接写出PC的范围.
,点B是线段PA外一点,PB=3,连接AB绕点A逆时针旋转90°得到线段AC,随着点B的位置变化,直接写出PC的范围.
【答案】(1)AD=BE,AD⊥BE;(2)AD=BE,AD⊥BE,理由见解析;(3)1≤PC≤5.
【解析】
(1)可先证明△ACE≌△BCD,再根据全等三角形的对应边相等可证得AE=BD,延长BD交AE于点F,由△ACE≌△BCD,再结合条件可得到∠ADF+∠FAD=90°,可得到AE⊥BD;
(2)仿照(1)先证明△ACE≌△BCD,可得AE=BD,再转换得到∠BOH+∠OBH=90°,可得到AE⊥BD;
(3)如图3中,作AE⊥AP,使得AE=PA,则易证△APE≌△ACP,可得PC=BE,求出BE的范围即可解决问题.
解:(1)结论:AD=BE,AD⊥BE,
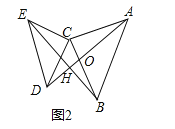
理由:如图1中,
∵△ACB与△DCE均为等腰直角三角形,
∴AC=BC,CE=CD,
∠ACB=∠ACD=90°,
在△ACD和△BCE中
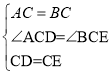
∴△ACD≌△BCE(SAS),
∴AD=BE,∠EBC=∠CAD,
延长BE交AD于点F,
∵BC⊥AD,
∴∠EBC+∠CEB=90°,
∵∠CEB=AEF,
∴∠EAD+∠AEF=90°,
∴∠AFE=90°,即AD⊥BE,
∴AD=BE,AD⊥BE,
故答案为AD=BE,AD⊥BE;
(2)结论:AD=BE,AD⊥BE,
理由:如图2中,设AD交BE于H,AD交BC于O,
∵△ACB与△DCE均为等腰直角三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=90°,
∴ACD=∠BCE,
在△ACD和△BCE中
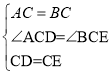
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CAD=∠CBE,
∵∠CAO+∠AOC=90°,∠AOC=∠BOH,
∴∠BOH+∠OBH=90°,
∴∠OHB=90°,
∴AD⊥BE,
∴AD=BE,AD⊥BE;
(3)如图3中,作AE⊥AP,使得AE=PA,
∴∠EAP=90°,
∵连接AB绕点A逆时针旋转90°得到线段AC,
∴AB=AC,∠BAC=90°,
∴∠EAP+∠PAB=∠BAC+∠PAB,
∴∠EAB=∠PAC,
在△EAB和△PAC中
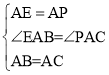
∴△EAB≌△PAC(SAS),
∴PC=BE,
∵PA=![]() ,
,
在等腰直角△PAE中,
PE=![]() ,
,

图3-1中,当P、E、B共线时,BE最小,最小值=PB-PE=1,
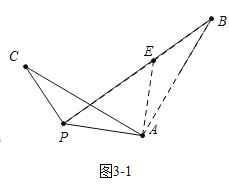
图3-2中,当P、E、B共线时,BE最大,最大值=PB+PE=5,
∴1≤BE≤5,即1≤PC≤5.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠PAQ=36°,点B为射线AQ上一固定点,按以下步骤作图:①分别以A,B为圆心,大于![]() AB的长为半径画弧,相交于两点M,N;②作直线MN交射线AP 于点D,连接 BD;③以B为圆心,BA长为半径画弧,交射线AP 于点C; 根据以上作图过程及所作图形,下列结论中错误的是( )
AB的长为半径画弧,相交于两点M,N;②作直线MN交射线AP 于点D,连接 BD;③以B为圆心,BA长为半径画弧,交射线AP 于点C; 根据以上作图过程及所作图形,下列结论中错误的是( )
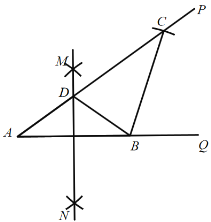
A.∠CDB=72°B.△ADB∽△ABCC.CD:AD=2:1D.∠ABC=3∠ACB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
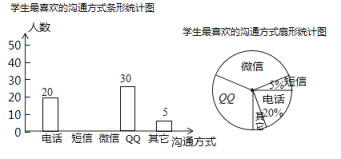
(1)这次统计共抽查了多少名学生?在扇形统计图中,表示" ![]() "的扇形圆心角的度数是多少;
"的扇形圆心角的度数是多少;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用 “微信”进行沟通的学生大约有多少名?
(4)某天甲、乙两名同学都想从“微信"、"![]() "、“电话"三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
"、“电话"三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有专家指出:人为型空气污染(如汽车尾气排放等)是雾霾天气的重要成因.某校为倡议“每人少开一天车,共建绿色家园”,想了解学生上学的交通方式.九年级(8)班的5名同学联合设计了一份调查问卷.对该校部分学生进行了随机调查.按A(骑自行车)、B(乘公交车)、C(步行)、D(乘私家车)、E(其他方式)设置选项,要求被调查同学从中单选.并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息,解答下列问题:
(1)本次接受调查的总人数是 人,扇形统计图中“骑自行车”所在扇形的圆心角度数是 度,请补全条形统计图;
(2)已知这5名学生中有2名女同学,要从这5名学生中任选两名同学汇报调查结果.请用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
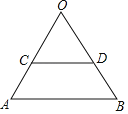
【题目】如图,△ABO是正三角形,CD∥AB,把△ABO绕△OCD的内心P旋转180°得到△EFG
(1)在图中画出点P和△EFG,保留画图痕迹,简要说明理由
(2)若AO=3![]() ,CD=2
,CD=2![]() ,求A点运动到E点路径的长.
,求A点运动到E点路径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,步行已成为人们最喜爱的健身方式之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现,小明步行消耗330000卡能量的步数与小红步行消耗300000卡能量的步数相同.已知小明平均每步消耗的能量比小红平均每步消耗的能量多3卡,求小红平均每步消耗能量的卡数.
查看答案和解析>>
科目:初中数学 来源: 题型:
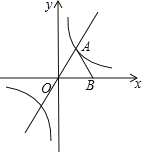
【题目】如图所示,在平面直角坐标系中,等边三角形OAB的一条边OB在x轴的正半轴上,点A在双曲线y=![]() (k≠0)上,其中点B为(2,0).
(k≠0)上,其中点B为(2,0).
(1)求k的值及点A的坐标
(2)△OAB沿直线OA平移,当点B恰好在双曲线上时,求平移后点A的对应点A’的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中
中![]() ,
,![]() 是
是![]() 的中点.请按要求完成下列作图,
的中点.请按要求完成下列作图,
①仅用无刻度直尺,不能用直尺中的直角;②保留作图痕迹
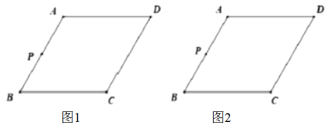
(1)在图1中,过点![]() 作
作![]() 的平行线,与
的平行线,与![]() 交于点
交于点![]() .
.
(2)在图2中,作线段![]() 的中垂线,垂足为点
的中垂线,垂足为点![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com