
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,连接
上一点,连接![]() 、
、![]() .
.![]() 为弧
为弧![]() 中点,过点
中点,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,且
,且![]() ,求
,求![]() 的半径.
的半径.

【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接OC.由点C为![]() 的中点,得到
的中点,得到![]() ,求得∠COB=∠COF,根据平行线的性质得到∠OCG=∠OMB=90°,于是得到CG是⊙O的切线;
,求得∠COB=∠COF,根据平行线的性质得到∠OCG=∠OMB=90°,于是得到CG是⊙O的切线;
(2)连接BC.由(1)知,∠COB=∠COF=![]() ∠BOF=60°,推出△OBC为等边三角形.得到∠OCD=30°,则EM=
∠BOF=60°,推出△OBC为等边三角形.得到∠OCD=30°,则EM=![]() CE=2,根据勾股定理得到CM=
CE=2,根据勾股定理得到CM=![]() ,求得OM=CM=
,求得OM=CM=![]() ,于是得到结论.
,于是得到结论.
(1)证明:连接OC.
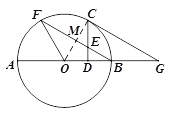
.∵点C为![]() 的中点,
的中点,
∴![]() ,
,
∴∠COB=∠COF,
∵OB=OF,
∴OC⊥BF,
设垂足为M,则∠OMB=90°,
∵CG∥FB,
∴∠OCG=∠OMB=90°,
∴CG是⊙O的切线;
(2)连接BC.
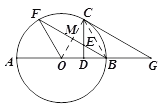
由(1)知,∠COB=∠COF=![]() ∠BOF=60°,
∠BOF=60°,
∵OB=OC,
∴△OBC为等边三角形.
∴∠OCD=30°,则EM=![]() CE=2,
CE=2,
∴CM=![]() .
.
根据等腰三角形“三线合一”得OM=CM=![]() ,
,
∴OC=4![]() ,
,
即⊙O的半径为4![]() .
.


科目:初中数学 来源: 题型:
【题目】对于一个函数,如果它的自变量 x 与函数值 y 满足:当1≤x≤1 时,1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,1)和点 B(1,1),则 a 的取值范围是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y = x2+bx+c过点A (-1,2),且关于y轴对称,点C与点B(a,0)(a>1)关于原点对称,直线AC交抛物线于点D.
(1)求此抛物线的解析式;
(2)连接OA,BD,当OA//BD时,求a的值;
(3)若直线AC交抛物线![]() 于E,F两点(点E在点F的左侧),且EA=DF,求直线AC的解析式.
于E,F两点(点E在点F的左侧),且EA=DF,求直线AC的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育文化用品商店购进篮球和排球共200个,进价和售价如下表全部销售完后共获利润2600元.
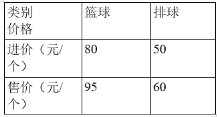
(1)求商店购进篮球和排球各多少个?
(2)王老师在元旦节这天到该体育文化用品商店为学校买篮球和排球各若干个(两种球都买了),商店在他的这笔交易中获利100元王老师有哪几种购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】智能手机如果安装了一款测量软件“SmartMeasure”后,就可以测量物高、宽度和面积等.如图,打开软件后将手机摄像头的屏幕准星对准脚部按键,再对准头部按键,即可测量出人体的高度.其数学原理如图②所示,测量者AB与被测量者CD都垂直于地面BC.若手机显示AC=1m,AD=1.8m,∠CAD=60°,求此时CD的高.(结果保留根号)
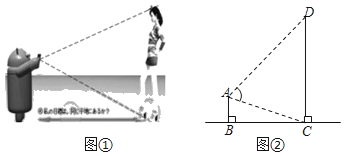
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“九月已经霜,蟹肥菊桂香”,古往今来,每至农历九月,蟹都是人们翘首以待的珍馐.某大闸蟹养殖户十月捕捞了第一批成熟的大闸蟹,并以每只相同的价格(价格为整数)批发给某经销商.十一月该养殖户捕捞了第二批成熟的大闸蟹,这次决定与某电商合作,将这批大闸蟹根据品质及重量分为A(小蟹)、B(中蟹)、C(大蟹)三类,每类按照不同的单价(价格都为整数)网上销售,若2只A类蟹、1只B类蟹和3只C类蟹的价格之和正好是第一批蟹8只的价格,而6只A类蟹、3只B类蟹和2只C类蟹的价格之和正好是第一批蟹12只的价格,且A类蟹与B类蟹每只的单价之比为3:4,根据市场有关部门的要求A、B、C三类蟹的单价之和不低于40元、不高于60元,则第一批大闸蟹每只价格为________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知二次函数![]() ,请你化成
,请你化成![]() 的形式_______,并在直角坐标系中画出
的形式_______,并在直角坐标系中画出![]() 的图像(列表、描点、连线);
的图像(列表、描点、连线);
(2)如果![]() 是函数图像上的两点,且
是函数图像上的两点,且![]() ,则
,则![]() ________
________![]() (填
(填![]() ,
,![]() 或
或![]() )
)
(3)若函数![]() 的图像与
的图像与![]() 轴没有交点,根据所画图像推断,实数
轴没有交点,根据所画图像推断,实数![]() 的取值范围为__________.
的取值范围为__________.
解:①、列表
| … | 0 | … | ||||
| … | 0 |
| 0 | … |
②描点、连线
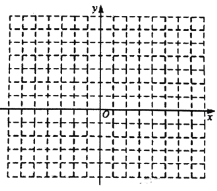
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线的顶点为![]() ,且经过点
,且经过点![]() ,与
,与![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点.
两点.
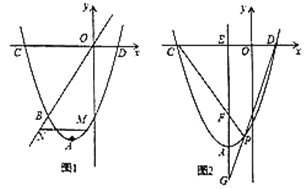
(1)求直线![]() 和抛物线的函数表达式;
和抛物线的函数表达式;
(2)如图,点![]() 是抛物线上的一个动点,且在直线
是抛物线上的一个动点,且在直线![]() 的下方,过点
的下方,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() ,求
,求![]() 的最大值;
的最大值;
(3)如图,过点![]() 的直线交
的直线交![]() 轴于点
轴于点![]() ,且
,且![]() 轴,点
轴,点![]() 是抛物线上
是抛物线上![]() 、
、![]() 之间的一个动点,直线
之间的一个动点,直线![]() 、
、![]() 与
与![]() 分别交于
分别交于![]() 、
、![]() 两点.当点
两点.当点![]() 运动时,
运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com