
分析 根据折叠得:GH是线段AB的垂直平分线,得出AG的长,再利用两角对应相等证△ACB∽△AGH,利用比例式可求GH的长,即折痕的长.
解答 解:如图,折痕为GH,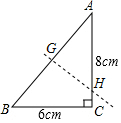
由勾股定理得:AB=$\sqrt{{6}^{2}+{8}^{2}}$=10cm,
由折叠得:AG=BG=$\frac{1}{2}$AB=$\frac{1}{2}$×10=5cm,GH⊥AB,
∴∠AGH=90°,
∵∠A=∠A,∠AGH=∠C=90°,
∴△ACB∽△AGH,
∴$\frac{AC}{AG}$=$\frac{BC}{GH}$,
∴$\frac{8}{5}$=$\frac{6}{GH}$,
∴GH=$\frac{15}{4}$cm.
故答案为:$\frac{15}{4}$.
点评 本题考查了折叠的性质和相似三角形的性质和判定,折叠是一种对称变换,它属于轴对称,本题的关键是明确折痕是所折线段的垂直平分线,利用三角形相似来解决.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
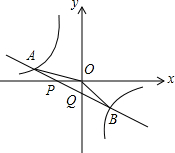 如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m)、B(1,n)两点,连接OA、OB.给出下列结论:
如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m)、B(1,n)两点,连接OA、OB.给出下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了( )步路(假设2步为1m),却踩伤了花草.
如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了( )步路(假设2步为1m),却踩伤了花草.| A. | 4 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小亮、小明两人星期天8:00同时分别从A,B两地出发,沿同一条路线前往新华书店C.小明从B地步行出发,小亮骑自行车从A地出发途经B地,途中自行车发生故障,维修耽误了1h,结果他俩11:00同时到达书店C.下图是他们距离A地的路程y(km)与所用时间x(h)之间的函数关系图象.请根据图中提供的信息,解答下列问题:
小亮、小明两人星期天8:00同时分别从A,B两地出发,沿同一条路线前往新华书店C.小明从B地步行出发,小亮骑自行车从A地出发途经B地,途中自行车发生故障,维修耽误了1h,结果他俩11:00同时到达书店C.下图是他们距离A地的路程y(km)与所用时间x(h)之间的函数关系图象.请根据图中提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
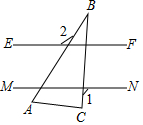 把含有30°的直角三角板(∠ABC=30°)如图放置,若EF∥MN,∠1=100°,则∠2的度数为( )
把含有30°的直角三角板(∠ABC=30°)如图放置,若EF∥MN,∠1=100°,则∠2的度数为( )| A. | 100° | B. | 120° | C. | 130° | D. | 150° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com