
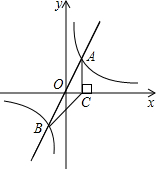
 如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,AC⊥x轴于点C,OC=3,连接BC.
如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,AC⊥x轴于点C,OC=3,连接BC.分析 (1)把A点横坐标代入正比例函数可求得A点坐标,代入反比例函数解析式可求得k,可求得反比例函数解析式;
(2)由条件可求得B、C的坐标,可先求得△ABC的面积,再结合△OPC与△ABC的面积相等求得P点坐标.
解答 解:(1)设A(3,a),
把x=3代入y=2x中,得y=2×3=6,
∴点A坐标为(3,6),
∵点A在反比例函数y=$\frac{k}{x}$的图象上,
∴k=3×6=18,
∴反比例函数的解析式为y=$\frac{18}{x}$;
(2)∵AC⊥OC,
∴OC=3,
∵A、B关于原点对称,
∴B点坐标为(-3,-6),
∴B到OC的距离为6,
∴S△ABC=2S△ACO=2×$\frac{1}{2}$×3×6=18,
∴S△OPC=18,
设P点坐标为(x,$\frac{18}{x}$),则P到OC的距离为|$\frac{18}{x}$|,
∴$\frac{1}{2}$×|$\frac{18}{x}$|×3=18,解得x=$\frac{3}{2}$或-$\frac{3}{2}$,
∴P点坐标为($\frac{3}{2}$,12)或(-$\frac{3}{2}$,-12).
点评 本题主要考查待定系数法求函数解析式及函数的交点问题,在(1)中求得A点坐标、在(2)中求得P点到OC的距离是解题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:选择题
| A. | a=1、b=2,c=$\sqrt{3}$ | B. | a=1、b=2,c=$\sqrt{5}$ | C. | a:b:c=3:4:5 | D. | ∠A:∠B:∠C=3:4:5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
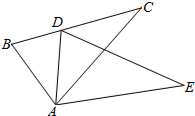 如图,在△ABC中,D是BC上一点,AB=AD,E是△ABC外一点,∠B=∠ADE,∠BAD=∠CAE.
如图,在△ABC中,D是BC上一点,AB=AD,E是△ABC外一点,∠B=∠ADE,∠BAD=∠CAE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 全等三角形的对应角都相等 | |
| B. | 如果两个实数相等,那么这两个实数的平方相等 | |
| C. | 对顶角相等 | |
| D. | 等边三角形每一个都等于60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
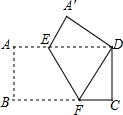 如图,把矩形ABCD沿EF翻折,点B恰好落在点D处,若AE=1,∠AEF=120°,则△DEF的面积是( )
如图,把矩形ABCD沿EF翻折,点B恰好落在点D处,若AE=1,∠AEF=120°,则△DEF的面积是( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 直线比曲线短 | B. | 两点确定一条直线 | ||
| C. | 两点之间直线最短 | D. | 两点之间线段最短 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com