
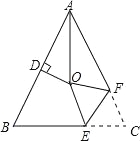
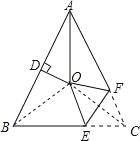
【题目】如图,△ABC中,AB=AC,∠BAC=54°,点D为AB中点,且OD⊥AB,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为 度.
【答案】108
【解析】
试题分析:连接OB、OC,根据角平分线的定义求出∠BAO,根据等腰三角形两底角相等求出∠ABC,再根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OB,根据等边对等角可得∠ABO=∠BAO,再求出∠OBC,然后判断出点O是△ABC的外心,根据三角形外心的性质可得OB=OC,再根据等边对等角求出∠OCB=∠OBC,根据翻折的性质可得OE=CE,然后根据等边对等角求出∠COE,再利用三角形的内角和定理列式计算即可得解.如图,连接OB、OC,∵∠BAC=54°,AO为∠BAC的平分线, ∴∠BAO=![]() ∠BAC=
∠BAC=![]() ×54°=27°,
×54°=27°,
又∵AB=AC, ∴∠ABC=![]() (180°﹣∠BAC)=
(180°﹣∠BAC)=![]() (180°﹣54°)=63°,
(180°﹣54°)=63°,
∵DO是AB的垂直平分线, ∴OA=OB, ∴∠ABO=∠BAO=27°,
∴∠OBC=∠ABC﹣∠ABO=63°﹣27°=36°, ∵AO为∠BAC的平分线,AB=AC,
∴△AOB≌△AOC(SAS), ∴OB=OC, ∴点O在BC的垂直平分线上,
又∵DO是AB的垂直平分线, ∴点O是△ABC的外心, ∴∠OCB=∠OBC=36°,
∵将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合, ∴OE=CE,∴∠COE=∠OCB=36°,
在△OCE中,∠OEC=180°﹣∠COE﹣∠OCB=180°﹣36°﹣36°=108°.


科目:初中数学 来源: 题型:
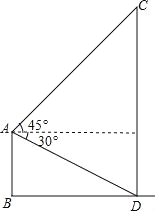
【题目】如图,平地上一个建筑物AB与铁塔CD相距60m,在建筑物的顶部测得铁塔底部的俯角为30°,测得铁塔顶部的仰角为45°,求铁塔的高度(![]() 取1.732,精确到1m).
取1.732,精确到1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将点A(a , -3)先向右平移2个单位长度,再向上平移4个单位长度得到点B(4,b),则a和b的值分别为( )
A. (1,4)
B. (4,1)
C. (2,1)
D. (1,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”
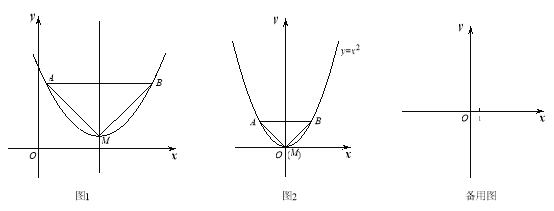
(1)①如图2,求出抛物线![]() 的“完美三角形”斜边AB的长;
的“完美三角形”斜边AB的长;
②抛物线![]() 与
与![]() 的“完美三角形”的斜边长的数量关系是 ;
的“完美三角形”的斜边长的数量关系是 ;
(2)若抛物线![]() 的“完美三角形”的斜边长为4,求a的值;
的“完美三角形”的斜边长为4,求a的值;
(3)若抛物线![]() 的“完美三角形”斜边长为n,且
的“完美三角形”斜边长为n,且![]() 的最大值为-1,求m,n的值.
的最大值为-1,求m,n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com