
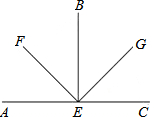
 如图,EF、EG分别是∠AEB、∠BEC的平分线,且EB为∠GEF的平分线,求∠GEF的度数,并写出∠BEF的余角和补角.
如图,EF、EG分别是∠AEB、∠BEC的平分线,且EB为∠GEF的平分线,求∠GEF的度数,并写出∠BEF的余角和补角. 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
| 5 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
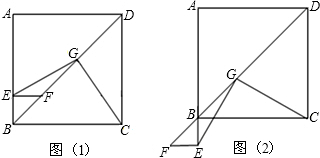 在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG、CG.
在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG、CG.查看答案和解析>>
科目:初中数学 来源: 题型:
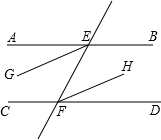 已知:如图,EF分别交于AB、CD于E、F,∠AEF=∠EFD,EG平分∠AEF,FH平分∠EFD.试说明EG∥FH成立的理由.
已知:如图,EF分别交于AB、CD于E、F,∠AEF=∠EFD,EG平分∠AEF,FH平分∠EFD.试说明EG∥FH成立的理由.| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市实验初级中学2011届九年级第二次模拟考试数学试题 题型:044
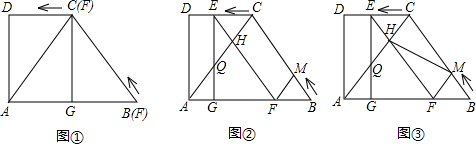
已知,如图
①,直角梯形ABCD,AB∥CD,∠A=90°,DC=6,AB=12,BC=10.Rt△EFG(∠EGF=90°)的边EF与BC完全重合,FG与BA在同一直线上.现将Rt△EFG以3 cm/s的速度水平向左作匀速平移(如图②),EF、EG分别交AC于点H、Q,同时点M以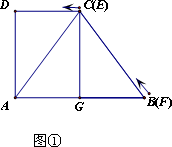
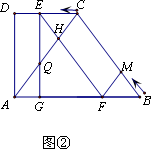
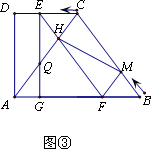
(1)当点Q是AC的中点时,求t的值;
(2)判断四边形CHFM的形状,并说明理由;
(3)如图③,连结HM,设四边形ABMH的面积为 s,求 s与t的函数关系式及 s的最小值.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
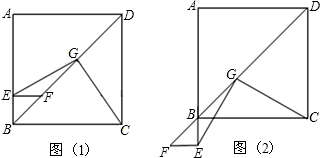
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com