
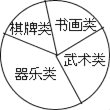
【题目】某校学生会准备调查六年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.
(1)确定调查方式时,甲同学说:“我到六年级(1)班去调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到六年级每个班随机调查一定数量的同学”.请指出哪位同学的调查方式最合理.
类别 | 频数(人数) | 频率 |
武术类 | 0.25 | |
书画类 | 20 | 0.20 |
棋牌类 | 15 | b |
器乐类 | ||
合计 | a | 1.00 |
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图.
请你根据以上图表提供的信息解答下列问题:
①a=_____,b=_____;
②在扇形统计图中,器乐类所对应扇形的圆心角的度数是_____;
③若该校六年级有学生560人,请你估计大约有多少学生参加武术类校本课程.
【答案】(1)见解析; (2)① a=100,b=0.15; ②144°;③140人.
【解析】
(1)采用随机调查的方式比较合理,随机调查的关键是调查的随机性,这样才合理;
(2)①用喜欢书画类的频数除以喜欢书画类的频率即可求得a值,用喜欢棋牌类的人数除以总人数即可求得b值.②求得器乐类的频率乘以360°即可.③用总人数乘以喜欢武术类的频率即可求喜欢武术的总人数.
(1)∵调查的人数较多,范围较大,
∴应当采用随机抽样调查,
∵到六年级每个班随机调查一定数量的同学相对比较全面,
∴丙同学的说法最合理.
(2)①∵喜欢书画类的有20人,频率为0.20,
∴a=20÷0.20=100,
b=15÷100=0.15;
②∵喜欢器乐类的频率为:1﹣0.25﹣0.20﹣0.15=0.4,
∴喜欢器乐类所对应的扇形的圆心角的度数为:360×0.4=144°;
③喜欢武术类的人数为:560×0.25=140人.


科目:初中数学 来源: 题型:
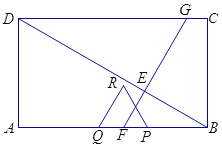
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为对角线
为对角线![]() 上一点,且
上一点,且![]() ,过
,过![]() 作
作![]() ,分别交
,分别交![]() 、
、![]() 于
于![]() 、
、![]() 。动点
。动点![]() 从点
从点![]() 出发,以每秒1个单位长的速度在射线
出发,以每秒1个单位长的速度在射线![]() 上运动。动点
上运动。动点![]() 从点
从点![]() 出发,以每秒1个单位长的速度在线段
出发,以每秒1个单位长的速度在线段![]() 上沿
上沿![]()
![]()
![]() 方向运动。以
方向运动。以![]() 为边作等边
为边作等边![]() 。已知
。已知![]() 、
、![]() 两点同时出发,当点
两点同时出发,当点![]() 返回点
返回点![]() 时两点同时停止运动。运动时间为
时两点同时停止运动。运动时间为![]() 秒.
秒.
(1)求线段![]() ,当点
,当点![]() 落在线段
落在线段![]() 上时
上时![]() 等于多少;
等于多少;
(2)设运动过程中![]() 与矩形
与矩形![]() 的重叠部分面积为
的重叠部分面积为![]() ,请直接写出
,请直接写出![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
(3)将四边形![]() 绕点
绕点![]() 旋转一周,在此过程中,设直线
旋转一周,在此过程中,设直线![]() 分别与直线
分别与直线![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,当
,当![]() 是以
是以![]() 为底角的等腰三角形时,求
为底角的等腰三角形时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,同时点
的速度移动,同时点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.当一个点到达终点时另一点也随之停止运动,设运动时间为
的速度移动.当一个点到达终点时另一点也随之停止运动,设运动时间为![]() 秒,
秒,

![]() 求几秒后,
求几秒后,![]() 的面积等于
的面积等于![]() ?
?
![]() 求几秒后,
求几秒后,![]() 的长度等于
的长度等于![]() ?
?
![]() 运动过程中,
运动过程中,![]() 的面积能否等于
的面积能否等于![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
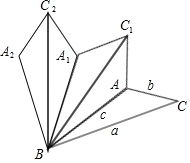
【题目】在△ABC中,∠ABC<20°,三边长分别为a,b,c,将△ABC沿直线BA翻折,得到△ABC1;然后将△ABC1沿直线BC1翻折,得到△A1BC1;再将△A1BC1沿直线A1B翻折,得到△A1BC2;…,若翻折4次后,得到图形A2BCAC1A1C2的周长为a+c+5b,则翻折11次后,所得图形的周长为_____________.(结果用含有a,b,c的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南水北调中线工程的起点是丹江口水库,按照工程计划,需对原水库大坝进行混凝土培厚加高,使坝高由原来的162米增加到176.6米,以抬高蓄水位,如图是某一段坝体加高工程的截面示意图,其中原坝体的高为BE,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡底端水平方向增加的宽度AC.(结果精确到0.1米,参考数据:sin 68°≈0.93,cos 68°≈0.37,tan 68°≈2.5,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
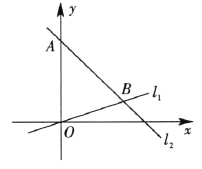
【题目】如图,在平面直角坐标系内,点![]() 的坐标为(0,24),经过原点的直线
的坐标为(0,24),经过原点的直线![]() 与经过点
与经过点![]() 的直线
的直线![]() 相交于点
相交于点![]() ,点
,点![]() 的坐标为(18,6).
的坐标为(18,6).
(1)求直线![]() ,
,![]() 对应的函数表达式;
对应的函数表达式;
(2)点![]() 为线段
为线段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 重合),作
重合),作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,设点
,设点![]() 的纵坐标为
的纵坐标为![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=![]() ,AH=
,AH=![]() ,求EM的值.
,求EM的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() ,连接
,连接![]() ,将
,将![]() 对折,点
对折,点![]() 落在直线
落在直线![]() 上的点
上的点![]() 处,得折痕
处,得折痕![]() ;将
;将![]() 对折,点
对折,点![]() 落在直线
落在直线![]() 上的点
上的点![]() 处,得折痕
处,得折痕![]() ,当
,当![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上时.若令
上时.若令![]() 的面积为
的面积为![]() ,
,![]() 的长度为
的长度为![]() ,则
,则![]() 关于
关于![]() 的函数解析式是( )
的函数解析式是( )
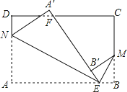
![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com