
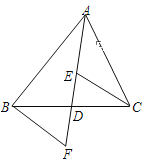
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:

(1)FC=AD;
(2)AB=BC+AD.
【答案】证明见解析
【解析】
试题分析:(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)根据线段垂直平分线的性质判断出AB=BF即可.
试题解析:证明:(1)∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
∵在△ADE与△FCE中,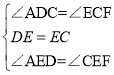 ,
,
∴△ADE≌△FCE(ASA),
∴FC=AD(全等三角形的性质).
(2)∵△ADE≌△FCE,
∴AE=EF,AD=CF(全等三角形的对应边相等),
∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF,
∵AD=CF(已证),
∴AB=BC+AD(等量代换).


科目:初中数学 来源: 题型:
【题目】如图:
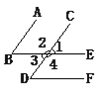
(1)如果∠1=∠B,那么_______∥_______,根据是__________________________;
(2)如果∠3=∠D,那么_______∥_______,根据是__________________________;
(3)如果要使BE∥DF,必须∠1=∠_______,根据是_________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小华在一起玩数字游戏,他们每人取了一张数字卡片,拼成了一个两位数. 小明说:“哇!这个两位数的十位数字与个位数字之和恰好是9.”他们又把这两张卡片对调,得到了一个新的两位数,小华说:“这个两位数恰好比原来的两位数大9.”那么,你能回答以下问题吗?
他们取出的两张卡片上的数字分别是多少?
第一次,他们拼成的两位数是多少?
第二次,他们拼成的两位数又是多少呢?请你好好动动脑筋哟!
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上一点,∠BOC=120°,OD平分∠AOC.
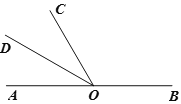
(1)求∠COD的度数.
请你补全下列解题过程.
∵点O为直线AB上一点,
∴∠AOB=_____.
∵∠BOC =120°,
∴∠AOC=______.
∵OD 平分∠AOC,
∴∠COD=![]() ∠AOC.( )
∠AOC.( )
∴∠COD=________.
(2)若E是直线AB外一点,满足∠COE:∠BOE=4:1直接写出∠BOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,﹣3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.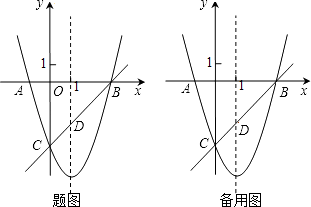
(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式;
(3)点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ= ![]() AB时,求tan∠CED的值;
AB时,求tan∠CED的值;
②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
温馨提示:考生可以根据第(3)问的题意,在图中补出图形,以便作答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值 x(x﹣1)+2x(x+1)﹣(3x﹣1)(2x﹣5),其中 x=2.
(2)解方程(3x﹣2)(2x﹣3)=(6x+5)(x﹣1)+15.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com