
”¾ĢāÄæ”æŹżÖįÉĻA£¬B£¬CČżµć¶ŌÓ¦µÄŹża£¬b£¬cĀś×ć(a+40)2+|b+10|£½0£¬BĪŖĻ߶ĪACµÄÖŠµć.

(1)Ö±½ÓŠ“³öA£¬B£¬C¶ŌÓ¦µÄŹża£¬b£¬cµÄÖµ.
(2)ČēĶ¼1£¬µćD±ķŹ¾µÄŹżĪŖ10£¬µćP£¬Q·Ö±š“ÓA£¬DĶ¬Ź±³ö·¢ŌČĖŁĻąĻņŌĖ¶Æ£¬µćPµÄĖŁ¶ČĪŖ6øöµ„Ī»/Ćė£¬µćQµÄĖŁ¶ČĪŖ1øöµ„Ī»/Ćė.µ±µćPŌĖ¶Æµ½CŗóŃøĖŁŅŌŌĖŁ·µ»Ųµ½AÓÖÕŪ·µĻņCµćŌĖ¶Æ£»µćQŌĖ¶ÆÖĮBµćŗóĶ£Ö¹ŌĖ¶Æ£¬Ķ¬Ź±PµćŅ²Ķ£Ö¹ŌĖ¶Æ.ĒóŌŚ“ĖŌĖ¶Æ¹ż³ĢÖŠP£¬QĮ½µćĻąÓöµćŌŚŹżÖįÉĻ¶ŌÓ¦µÄŹż.
(3)ČēĶ¼2£¬M£¬NĪŖA£¬CÖ®¼äĮ½µć(µćMŌŚN×ó±ß£¬ĒŅĖüĆĒ²»ÓėA£¬CÖŲŗĻ)£¬E£¬F·Ö±šĪŖAN£¬CMµÄÖŠµć£¬Ēó![]() µÄÖµ.
µÄÖµ.
”¾“š°ø”æ(1)a£½©40£¬b£½©10£¬c=20£»(2)P£¬QĮ½µćĻąÓöµćŌŚŹżÖįÉĻ¶ŌÓ¦µÄŹżĪŖ©4»ņ![]() £»(3)
£»(3)![]() =2.
=2.
”¾½āĪö”æ
(1)øł¾Ż(a+40)2+|b+10|£½0£¬æÉĒó³öa”¢bµÄÖµ£¬BĪŖĻ߶ĪACµÄÖŠµć.½ų¶ųæÉĒó³öcµÄÖµ£»
(2)·ÖĮ½ÖÖĒéæö½ųŠŠ½ā“š£¬Ņ»ÖÖŹĒŌŚA”¢DÖ®¼äŹ×“ĪĻąÓö£¬¶žŹĒµćPµ½Cŗó·µ»Ų×·¼°QĻąÓö£¬ÉčŌĖ¶ÆŹ±¼ä£¬øł¾ŻĻąÓö”¢×·¼°ĪŹĢāŹżĮæ¹ŲĻµĮŠ·½³ĢĒó³öŹ±¼ä£¬½ų¶ųĒó³öĻąÓ¦Ź±Ėł¶ŌÓ¦µÄŹż£»
(3)øł¾ŻĻ߶ĪµÄÖŠµćµÄŅāŅ壬ÓĆÖŠµćĻ߶ĪEF±ķŹ¾ACŗó¼“æÉµĆ³ö“š°ø.
½ā£ŗ(1)”ß(a+40)2+|b+10|£½0£¬
”ąa£½©40£¬b£½©10£¬
”ßBĪŖĻ߶ĪACµÄÖŠµć£¬
”ą![]() £½©10£¬
£½©10£¬
”ąc£½20£¬
¼“£ŗa£½©40£¬b£½©10£¬c£½20£»
(2)ČēĶ¼1£¬ÉčŌĖ¶ÆµÄŹ±¼äĪŖtĆė£¬
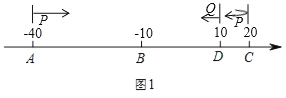
¢Łµ±PÓėQµŚŅ»“ĪĻąÓöŹ±£¬ÓŠ6t+t£½10©(©40)£¬
½āµĆ£¬t£½![]() £¬
£¬
“ĖŹ±ĻąÓöµć¶ŌÓ¦µÄŹżĪŖ10©![]() £½
£½![]() £»
£»
¢Śµ±µćPµ½C·µ»Ų×·ÉĻµćQŹ±£¬ÓŠ6t©60£½t+10£¬
½āµĆ£¬t£½14£¬
“ĖŹ±ĻąÓöµć¶ŌÓ¦µÄŹżĪŖ10©14£½©4£¬
“š£ŗŌŚ“ĖŌĖ¶Æ¹ż³ĢÖŠP£¬QĮ½µćĻąÓöµćŌŚŹżÖįÉĻ¶ŌÓ¦µÄŹżĪŖ©4»ņ![]() £»
£»
(3)ČēĶ¼2£¬”ßE£¬F·Ö±šĪŖAN£¬CMµÄÖŠµć£¬
”ąAN£½2EN£¬CM£½2MF£¬
”ąAC£½2EN+2MF©MN
”ą![]() £½
£½![]() £½
£½![]() £½
£½![]() £½2£¬
£½2£¬
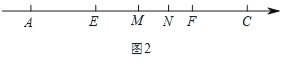


 53ĖęĢĆ²āĻµĮŠ“š°ø
53ĖęĢĆ²āĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
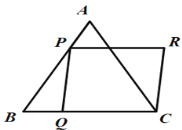
”¾ĢāÄæ”æČēĶ¼£¬µČ±ß”÷ABC±ß³¤ĪŖ4£¬µćP£¬Q·Ö±šŹĒAB,BC±ßÉĻµÄ¶Æµć£¬ĒŅAP =BQ= x,×÷”õPQCR£¬ŌņÓĆŗ¬xµÄ“śŹżŹ½±ķŹ¾”õPQCRµÄĆ껿ĪŖ______£»µ±PC”ĪARŹ±£¬ x =____.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ŠŠĖıߊĪABCDÖŠ£¬¹żµćB×÷BE”ĶCD£¬“¹×ćĪŖE£¬Į¬½įAE£¬FĪŖAEÉĻŅ»µć£¬ĒŅ”ĻBFE=”ĻC.
£Ø1£©ĒóÖ¤£ŗ ![]() £»
£»
£Ø2£©ČōAB=4£¬”ĻBAE=30”ć£¬ĒóAEµÄ³¤.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»Ź³ĢĆŠčŅŖ¹ŗĀņŗŠ×Ó“ę·ÅŹ³Īļ£¬ŗŠ×ÓÓŠA”¢BĮ½ÖÖŠĶŗÅ£¬µ„øöŗŠ×ÓµÄČŻĮæŗĶ¼ŪøńČē±ķøńĖłŹ¾£®ĻÖÓŠ15ÉżŹ³ĪļŠčŅŖ“ę·ÅĒŅŅŖĒóĆæøöŗŠ×Ó¶¼ŅŖ×°Āś£¬ÓÉÓŚAŠĶŗÅŗŠ×ÓÕż×ö“ŁĻś»ī¶Æ£ŗ¹ŗĀņČżøö¼°ČżøöŅŌÉĻæÉŅ»“ĪŠŌĆæøö·µ»¹ĻÖ½š1.5ŌŖ£¬ŌņøĆŹ³ĢĆ¹ŗĀņŗŠ×ÓĖłŠč×īÉŁ·ŃÓĆŹĒ__________£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŗ£ÖŠÓŠŅ»Š”µŗP£¬ŌŚ¾ąŠ”µŗPµÄ![]() ŗ£Ąļ·¶Ī§ÄŚÓŠ°µ½ø£¬Ņ»ĀÖ“¬×ŌĪ÷Ļņ¶«ŗ½ŠŠ£¬ĖüŌŚA“¦Ź±²āµĆŠ”µŗPĪ»ÓŚ±±Ę«¶«60”ć£¬ĒŅA”¢PÖ®¼äµÄ¾ąĄėĪŖ32ŗ£Ąļ£¬ČōĀÖ“¬¼ĢŠųĻņÕż¶«·½Ļņŗ½ŠŠ£¬ĀÖ“¬ÓŠĪŽ“„½øĪ£ĻÕ£æĒėĶعż¼ĘĖć¼ÓŅŌĖµĆ÷£®Čē¹ūÓŠĪ£ĻÕ£¬ĀÖ“¬×ŌA“¦æŖŹ¼ÖĮÉŁŃŲ¶«Ę«ÄĻ¶ąÉŁ¶Č·½Ļņŗ½ŠŠ£¬²ÅÄÜ°²Č«ĶعżÕāŅ»ŗ£Óņ£æ
ŗ£Ąļ·¶Ī§ÄŚÓŠ°µ½ø£¬Ņ»ĀÖ“¬×ŌĪ÷Ļņ¶«ŗ½ŠŠ£¬ĖüŌŚA“¦Ź±²āµĆŠ”µŗPĪ»ÓŚ±±Ę«¶«60”ć£¬ĒŅA”¢PÖ®¼äµÄ¾ąĄėĪŖ32ŗ£Ąļ£¬ČōĀÖ“¬¼ĢŠųĻņÕż¶«·½Ļņŗ½ŠŠ£¬ĀÖ“¬ÓŠĪŽ“„½øĪ£ĻÕ£æĒėĶعż¼ĘĖć¼ÓŅŌĖµĆ÷£®Čē¹ūÓŠĪ£ĻÕ£¬ĀÖ“¬×ŌA“¦æŖŹ¼ÖĮÉŁŃŲ¶«Ę«ÄĻ¶ąÉŁ¶Č·½Ļņŗ½ŠŠ£¬²ÅÄÜ°²Č«ĶعżÕāŅ»ŗ£Óņ£æ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖÖ±Ļß![]() ¾¹żµć
¾¹żµć![]() £¬
£¬![]() £®
£®

£Ø1£©ĒóÖ±Ļß![]() µÄ½āĪöŹ½£»
µÄ½āĪöŹ½£»
£Ø2£©ČōÖ±Ļß![]() ÓėÖ±Ļß
ÓėÖ±Ļß![]() Ļą½»ÓŚµć
Ļą½»ÓŚµć![]() £¬Ēóµć
£¬Ēóµć![]() µÄ×ų±ź£»
µÄ×ų±ź£»
£Ø3£©øł¾ŻĶ¼Ļó£¬Ö±½ÓŠ“³ö¹ŲÓŚ![]() µÄ²»µČŹ½
µÄ²»µČŹ½![]() µÄ½ā¼Æ£®
µÄ½ā¼Æ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ŌŚĘ½ŠŠĖıߊĪABCDÖŠ£¬CD£½2AD£¬BE”ĶAD£¬µćFĪŖDCÖŠµć£¬Į¬½ÓEF”¢BF£¬ĻĀĮŠ½įĀŪ£ŗ¢Ł”ĻABC£½2”ĻABF£»¢ŚEF£½BF£»¢ŪSĖıߊĪDEBC£½2S”÷EFB£»¢Ü”ĻCFE£½3”ĻDEF£¬ĘäÖŠÕżČ·µÄÓŠ_____£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
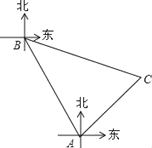
”¾ĢāÄæ”æijŗ£ÓņÓŠA”¢BĮ½øöøŪæŚ£¬BøŪæŚŌŚAøŪæŚ±±Ę«Ī÷30”ć·½ĻņÉĻ£¬¾ąAøŪæŚ60ŗ£Ąļ£¬ÓŠŅ»ĖŅ“¬“ÓAøŪæŚ³ö·¢£¬ŃŲ¶«±±·½ĻņŠŠŹ»Ņ»¶Ī¾ąĄėŗ󣬵½“ļĪ»ÓŚBøŪæŚÄĻĘ«¶«75”ć·½ĻņµÄC“¦£¬Ēó£ŗ
£Ø1£©”ĻC=”” ”””ć£»
£Ø2£©“ĖŹ±æĢ“¬ÓėBøŪæŚÖ®¼äµÄ¾ąĄėCBµÄ³¤£Ø½į¹ū±£ĮōøłŗÅ£©£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ŠŠĖıߊĪABCDÖŠ£¬AB=6£¬”ĻBADµÄĘ½·ÖĻßÓėBCµÄŃÓ³¤Ļß½»ÓŚµćE”¢ÓėDC½»ÓŚµćF£¬ĒŅµćFĪŖ±ßDCµÄÖŠµć£¬”ĻADCµÄĘ½·ÖĻß½»ABÓŚµćM£¬½»AEÓŚµćN£¬Į¬½ÓDE
(1) ĒóÖ¤£ŗBC=CE
(2) ČōDM=2£¬ĒóDEµÄ³¤

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com