
 作图、证明与计算
作图、证明与计算| 1 |
| 2 |
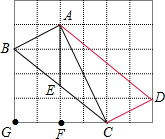 解:(1)如图所示;
解:(1)如图所示;| 42+32 |
| 5 |
| CD |
| AD |
| ||
| 5 |
| 2 |
| 4 |
| 1 |
| 2 |
| BC |
| 2 |
| 5 |
| 2 |
| 5 |
| 5 |
| 1 |
| 2 |
3
| ||
| 2 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
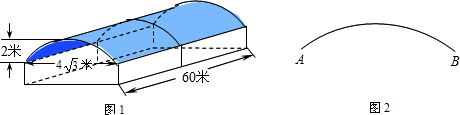
 如图AB、CD是两条垂直的公路,设计时想在拐弯处用一段圆弧形弯道把它们连接起来(圆弧在B、D两处分别与道路相切),测得BC=100米,∠PBC=45°.
如图AB、CD是两条垂直的公路,设计时想在拐弯处用一段圆弧形弯道把它们连接起来(圆弧在B、D两处分别与道路相切),测得BC=100米,∠PBC=45°.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:湖北省咸宁市2012年中考数学试题 题型:044
如图1,矩形MNPQ中,点E,F,G,H分别在NP,PQ,QM,MN上,若∠1=∠2=∠3=∠4,则称四边形EFGH为矩形MNPQ的反射四边形.图2,图3,图4中,四边形ABCD为矩形,且AB=4,BC=8.
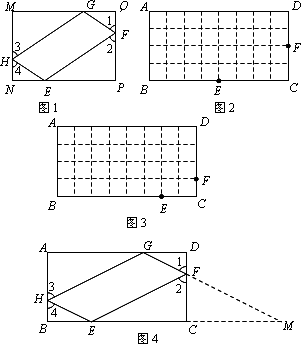
理解与作图:
(1)在图2,图3中,点E,F分别在BC,CD边上,试利用正方形网格在图上作出矩形ABCD的反射四边形EFGH.
计算与猜想:
(2)求图2,图3中反射四边形EFGH的周长,并猜想矩形ABCD的反射四边形的周长是否为定值?
启发与证明:
(3)如图4,为了证明上述猜想,小华同学尝试延长GF交BC的延长线于M,试利用小华同学给我们的启发证明(2)中的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com